――数理工学を、錯視以外にもさまざまな分野に応用されています。数理を適用する観点で、学問分野による違いはありますか。
原理がわかって基本方程式から解ける分野と、原理はわからないが、目的によってそれなりに使える方程式を見つけていく分野の2つがあると思います。前者は、力学や電磁気学などで、この方程式を大規模に利用して成功している例の1つが最近の天気予報です。一方、生物学や進化、社会科学などは、基本方程式がわからない分野です。
錯視の場合は、ものを見るのは光学的な原理のわかる分野、それを認識するのはメカニズムが未解明の分野という組み合わせです。ただ、錯視では、原理未解明の部分も、実験を繰り返して解明が進められます。その点、経済学は、事象が1回限りで再現できないから難しいですが、数理の適用をあきらめるべきではない。過信を戒めつつ、一定の論理を立て、それを検証していくべきと思います。
――英語論文の書き方、プログラミング、子供向けの啓発記事など、後進の育成のための著作にも注力されています。
はい。とても便利で、知っておくと得ですよ、というメッセージです。自分が学んで有益だったことを、どうしても書きたくなる。教育では、数学が物事を理解する力を持っているだけでなく、新しいものを作り出す力もあることを伝えたいのです。高校生から、「数学は何の役に立つのか」と聞かれる先生が多いと聞きます。そのとき、役に立つと知ってもらう意義は大きい。数学が好きな生徒は、そうすればもっと勉強しようと思うはずです。
錯視は、不思議さで興味を呼びます。数学でこれが作れると知れば、勉強する意欲が刺激されるでしょう。高校からの講演依頼を多くいただきますが、極力応じるようにしています。最近も依頼があり、札幌で全校生徒を集めた講演をします。
自分にしか書けない本を書く
――「ボロノイ図のバイブル」と言われる名著を書かれ、世界でも有名だそうですが、ボロノイ図とは何ですか?
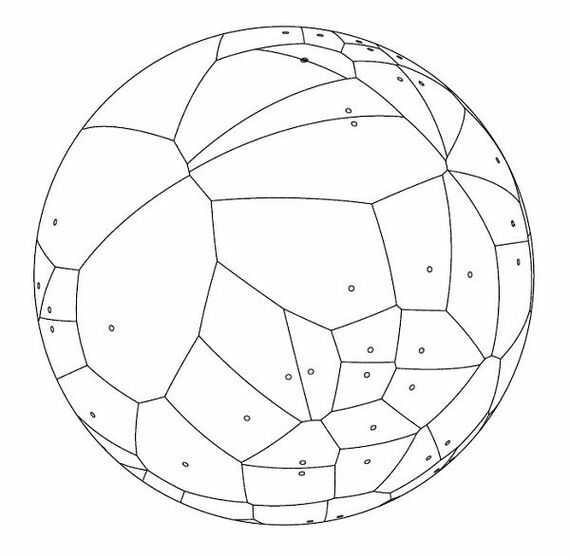
ボロノイ図は、「勢力圏図」と考えてもらうといいでしょう。平面または曲面上に置かれた拠点からの距離で領域を分割したものです。
工学では、さまざまな計算に偏微分方程式が用いられますが、このボロノイ図は、偏微分方程式を解く際にたいへん役立ちます。コンピュータは、領域をメッシュという小さな三角形に分けて近似計算を行いますが、そのとき、ボロノイ図を利用すると計算精度が高い最適なメッシュが得られるのです。
また、より平明な応用例では、救急車が直線でなく道のりで到達することを前提に、どこの拠点からどの地区をカバーするのがよいか、といった問題にも使えます。
































無料会員登録はこちら
ログインはこちら