数学を｢日常で不要｣と嫌う人が知らない真の魅力 算数と数学を同一視していると見えてこない

次は「数学の美しさ」が感じられる例を出してみましょう。

数学Aの「図形の性質」で学ぶ「オイラーの多面体定理」を紹介します。オイラーの多面体定理は、すべての多面体に共通する非常に“美しい”性質を示しています。

幾何学を学ぶ意義は、実利的には論理的な考え方を身につけることにあるのですが、実をいうと、私はもう1つ幾何学を学ぶ意義があると思っています。それは、数学の“美しさ”を感じるということです。

美しさという主観的な言葉は、数学には似つかわしくないと思われるかもしれません。が、数学的でありたいと願う心は、美しくありたいと願う心にとてもよく似ています。私が考える数学の美しさとは「対称性」「合理性」「意外性」「簡潔さ」です。

オイラーの多面体定理にはこのすべてがあります。

方法はどうであれ必ず正しい結論にたどりつく

辞書（広辞苑）を引くと「美」とは「知覚・感覚・情感を刺激して内的快感をひきおこすもの」とあります。美しさの中に合理性が入っているのは、私にとってはそれが快感だからです。合理的に導かれた結論はどういう筋道を通って導かれても、いつも同じになります。合理的でありさえすれば、自由に考えることが許されるのです。

例えば、三平方の定理（ピタゴラスの定理）には100通り以上も証明方法があるといわれていますが、数学ではプロセスさえ正しければ、方法はどうであれ必ず正しい結論にたどりつきます。それはとても気持ちのいいことです。

数学に限らず多くの科学者が研究に没頭するのは、そこに美しさがあるからだと私は思います。

さて、オイラーの多面体定理は以下の式で表されます。

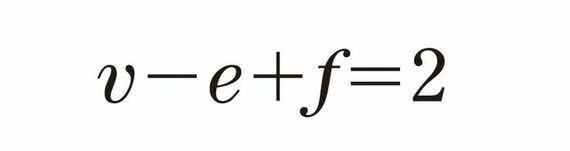
vは頂点のvertex、eは辺のedge、fは面のfaceです。正多面体に限らず、任意の多面体の頂点と辺と面の数について、v-e+f=2の関係がつねに成立するというのはとても不思議だと思いませんか。

ただし、任意の多面体とはいっても凸多面体ということにしておいてください（ドーナツのような「穴」が空いていなければ、凹多面体でもオイラーの多面体定理は成立します）。厳密な証明ではないのですが、この定理の雰囲気を味わってもらうために次のような思考実験をしてみましょう。