数学を｢日常で不要｣と嫌う人が知らない真の魅力 算数と数学を同一視していると見えてこない

まず、次のような四面体を用意します。正四面体でなくてもかまいません。この四面体の頂点、辺、面の数を数えてみましょう。頂点は4、辺は6、面は4ですから、v-e+fは確かに2になります。

出所：『教養としての「数学Ⅰ・A」』

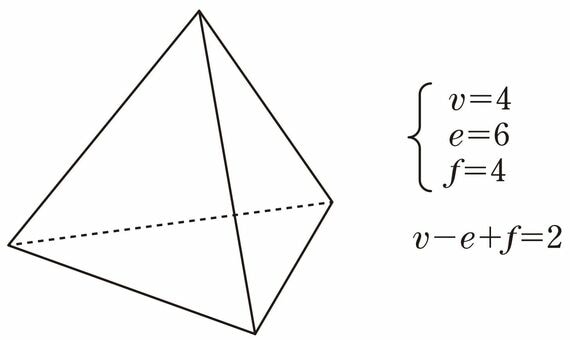
新しい頂点を1つ増やしてみると……

次に、ここから頂点を増やしてより複雑な多面体をつくってみます。以下のように、新しい頂点を1つ増やすと、いびつな形の多面体ができました。この多面体の頂点、辺、面の数をそれぞれv′、e′、f′とします。

出所：『教養としての「数学Ⅰ・A」』

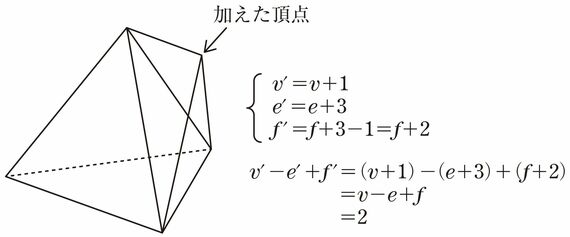
新たな図形における頂点の数は、最初の四面体よりも1個分増えていますから、＋1。辺の数はどうなるかといえば、頂点が増えたことによって3本増えましたから、＋3。面については、裏側と手前と下側で3つ増えましたが、消えた面が1つありますから＋2。

『教養としての「数学I・A」』（NHK出版）。書影をクリックするとAmazonのサイトにジャンプします。

こうしてv′－e′＋f′をつくってみると、やはり2になっています。また次の新しい頂点を増やせば、同じように頂点、面、辺の数が変化して、結局その合計は2になることがわかります。

つまり、少なくとも四面体から頂点を増やすことでつくられる立体については、オイラーの多面体定理が成立するということです。

この定理を発見したオイラーは18世紀の大数学者ですが、立体図形についてこんなにもシンプルな法則をそれまでの偉大な数学者たちの誰もが見逃していたということに、オイラー自身とても驚いたと伝えられています。

しかもこのオイラーの多面体定理は、今日でいうところのトポロジー（位相幾何学）に発展しました。「ゴム膜の幾何学」とも呼ばれるトポロジー理論は、現代のAIにも欠かせない非常に重要な理論となっています。