数学を｢日常で不要｣と嫌う人が知らない真の魅力 算数と数学を同一視していると見えてこない

誤解を恐れずにいえば、算数は生活能力です。いわゆる「読み・書き・算盤（そろばん）」の算盤にあたります。生活では「結局いくらなのか」という結果が求められるので、算数は、すでにやり方がわかっている問題を素早く正確に解けるよう訓練するための教科です。

3割引だといくら安くなるか計算したり、4人分のレシピを見て3人分の料理をつくったり、時速80kmで走っているなら20km先のサービスエリアまであと何分かかるか計算できたり、といった具合です。

数学は「未知の問題を解決する方法」を学ぶ教科

一方の数学は、未知の問題を解決する方法を学ぶ教科です。16世紀ごろ、イタリアのカルダノやフォンタナらが中心となって方程式の「解の公式」を見つけようと、大勢の数学者が夢中になりました。

どんな2次方程式でも解ける公式があるのだから、3次や4次の方程式にもそうした公式があるのでないか。そうやって、次々と解の公式が見つかっていきます。ちなみに5次方程式以上では解の公式が存在しないのですが、それを証明するために今度は「群論」と呼ばれる分野の手法が使われることになりました。数学は、いつも未知の問題に取り組んできました。

一般に成り立つ命題を積みあげていき、そこで得た知見を元に、未知の問題に挑む。そういう演繹的思考で、未知の問題に立ち向かうことが数学の醍醐味といえます。

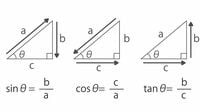
例えば、「余弦定理」は直角三角形でしか使えない三平方の定理（ピタゴラスの定理）から出発し、直角三角形以外の三角形についても辺の長さや面積を求められるよう、一般化を積み重ねていったものということになります。

そういった先人のたちの試行錯誤を追体験し、未知の問題に取り組むための思考訓練を行うのが、高校数学の目的なのです。