数学を｢日常で不要｣と嫌う人が知らない真の魅力 算数と数学を同一視していると見えてこない

数学的思考が味わえる身近な例として、数学Aで習う「条件付き確率」をとりあげてみましょう。

一般にある事象Aが起きたという前提のもとに事象Bが起きる確率のことを「条件付き確率」といい、以下のように表します。

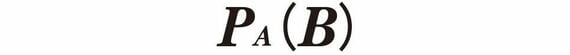
（外部配信先では図や画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

なお「事象」とは「確率が求められる事柄」のことです。

条件付き確率の面白いところは、結論が直観に反したものになるケースが多いということです。試しに次のような問題を考えてみましょう。

もし99％確かな検査で不治の病だといわれてしまったら、動揺し絶望してしまう人も多いのではないでしょうか。しかし、実はこのような検査結果になったとしてもまったく絶望する必要はありません。

真に陽性である人の確率は約1％

次の図をみてください。

出所：『教養としての「数学Ⅰ・A」』

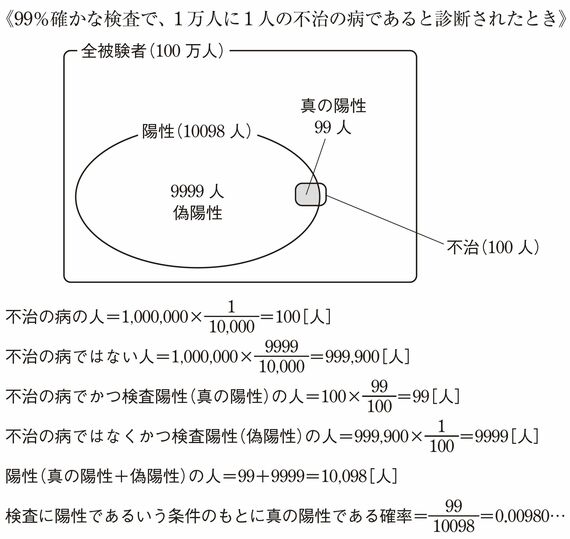
ここでは全被験者が100万人だとします。このうち、実際に不治の病になっている人は、1万人に1人ですから100万人の場合、100人です。

逆に、不治の病ではない人は99万9900人もいることになります。検査は99％確かなので、本当に病にかかっている人のうち99人が陽性だといわれます。一方、本当は病気ではないのに検査では陽性だといわれる人、いわゆる偽陽性者は、どれだけいるでしょうか。

99％確かな検査ですから、1％の人が誤った判定を受けます。本当は不治の病でない99万9900人のうち、9999人は陽性だといわれてしまうわけです。結局、この検査で陽性になる人は、本当の病になっている99人と、偽陽性の9999人を合わせて、1万98人になります。

1万98人の中で本当に陽性の人はわずか99人ですから、その確率は0.98％ぐらいでしかありません。もしこの検査で陽性だといわれても、あわてずに、精密検査を受けたほうがいいでしょう。

新型コロナウイルスのパンデミックでは、PCR検査の実施をめぐって大きな混乱が起きました。これも「条件付き確率」で考えれば、闇雲に検査数を増やせばいいというわけではないことがわかります。もし検査対象者を無症状の人にまでむやみに広げていくと、偽陽性者も増えていくため、医療資源を圧迫し、病院のキャパシティを超え、必要な人に医療が届かないということにつながりかねません。

なお、先ほどの例では、1万人に1人の不治の病としましたが、「100人に1人」に変えると結果は大きく変わってきます。この場合、陽性と診断されて、なおかつ本当に病である確率は50％に跳ね上がることになります。