｢究極の数学｣は驚くほどエレガントで力強い 青木薫が味わうNHK数学ミステリー白熱教室

そんなフレンケル教授がいったいどんな講義をするのだろうかと、わたしはわくわくしながら放映を待った。番組が始まってまず思ったのは、「やっぱり、フレンケルってイケメンだわぁ」ということだった。ド・アップに絶える端正な顔立ち。チャーミングな笑顔に思わず引き込まるし、手指の動きにふと目を奪われてしまう。いやあ、静止画像で見るより、動くフレンケルの方がずっと素敵だわぁ……。

しかし！そんなところに気をとられて、彼の話を聞き漏らすのはもったいない（と、我に返った）！

数学は宇宙の普遍言語なのか

わたしがハッとさせられたのは、番組の冒頭近く、「数学は宇宙の普遍言語なのだろうか？」という話題のところだ。宇宙人も、われわれと同じ数学の世界を共有していて、数学という言語を使えばコミュニケーションを取ることができるのだろうか。

フレンケルは、スタニスワフ・レムのSF『ソラリス』を例にもち出した。惑星ソラリスでは、ひとつの世界がまるごとひとつの存在なので、複数のものを、「ひとつ、ふたつ、みっつ」と数えるということがない。それゆえソラリスは自然数（1、2、3、……）の概念をつかむことができず、ひいては数学の発展も望めないだろう、という議論があるのだそうだ。

惑星ソラリスは惑星自身がひとつの生命体だが、自分の周りの軌道を衛星が何周するかで自然数を考える。逆周りがマイナスの整数となる

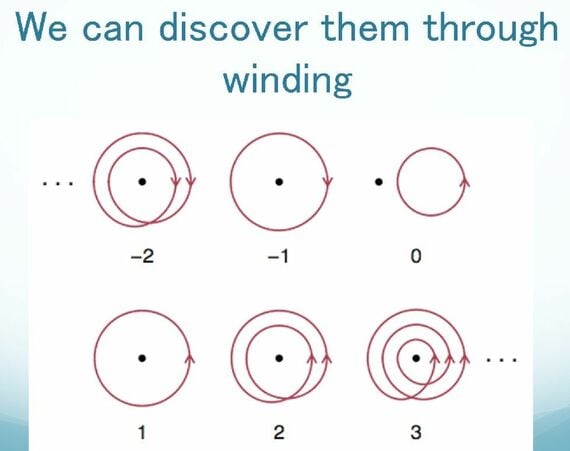
それに対して、数学は宇宙の普遍言語だと信じるフレンケルは、ソラリスであっても自然数の概念をつかめるということ（そして数学を発展させることができること）を、論証してみようと言い出した。

そのためにフレンケルが持ち出したのは、ありふれたデンタルフロスだ。そして彼は、フロスを指に巻きつけていく。ぐるり、ぐるり、ぐるり、と巻きつけていくと、1回、2回、3回、と巻きの回数を定義でき、それゆえ1、2、3という自然数の概念を把握できる。そればかりが、この方法では、逆向きに巻きつけていくことにより、－1、－2、－3、という負の数の概念が、ごく自然に得られるのだ。

わたしはこれまで、自然数の概念は、皿に盛られたイチゴのような対象を、1、2、3、と数えるなかで生まれたという、ごく一般的な説明だけで満足しきっていたので、この「糸巻き法」には不意をつかれた。そして、なんてエレガントなんだろうと、目が覚める思いがした。それはなんとも刺激的な感覚だった。