ド文系こそ知るべき偉大な｢微分･積分｣のヒミツ 300トン以上の飛行機が飛べるのも微分･積分のおかげ

このような複雑な状況を扱うために、微分積分が活躍します。

具体的な手順としては、図表4－2のように飛行機周辺の空間をコンピューター上で小さなブロックに切り分け、ブロックごとに気圧を計算します。気圧の計算が重要なのは、羽の上側と下側の気圧差から生じる力（＝揚力）によって羽が上向きの力を受け、それによって飛行機が浮かんでいるからです。

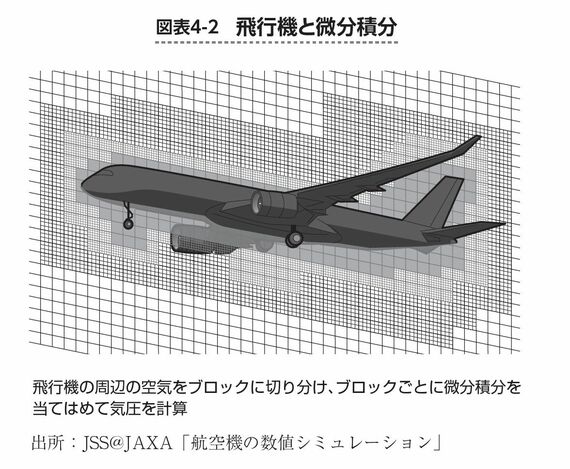
ちなみに、図表4－2をよく見ると、飛行機の機体に近いところほど格子が細かくなっていますね。これは、飛行機から離れたところの空気の流れよりも、飛行機のすぐそばの空気の流れの方がより重要なので、ブロックをより細かくして計算を正確にしているからです。

飛行機が飛ぶのも微分積分のおかげ

気圧を計算するためには、ブロックごとの空気の出入りを把握する必要があります。例えば、あるブロックに入ってくる空気の量が出ていく量よりも多ければ、そのブロックにおける空気の密度が上昇し、気圧が上がります。

これは電車の混み具合と対比させて考えるとわかりやすいかもしれません。朝の通勤ラッシュでは、乗ってくる人数が降りていく人数より多いために車両内の人口密度が高まっていきますが、それと同じようなイメージです。

逆に、通勤時間帯を過ぎれば、乗ってくる人数より降りていく人数の方が多くなるので、車両内の人口密度が下がっていきます。同様に、あるブロックに入ってくる空気の量よりも出ていく量の方が多ければ、そのブロックにおける空気の密度が低下するため、気圧が下がります。

このように「小さなブロックへの空気の出入り」という問題に落とし込むことで、コンピューターを使った計算が可能になります。

『見るだけでわかる微分・積分』（PHP研究所）。書影をクリックするとAmazonのサイトにジャンプします

小さなブロックに切り分けるという方法には、小さく刻むことで単純化するという微分の考え方が活かされています。けれども、単に小さなブロックに切り分けただけでは、そのブロックへの空気の出入りをどうやって計算するのかという課題が残ってしまいます。

そこで、もう一段踏み込んだ単純化を行います。微分の考え方を使ってさらに「時間」も短く切り刻むのです。

小さなブロックに区切ることで単純化（＝微分の考え方）し、さらに、短い時間を考えることでもう一段の単純化（＝微分の考え方）を行うという、2段構えで微分の考え方を適用しているのです。

ブロックごとの気圧の計算が終わったあとは、計算結果を足し合わせることで元に戻します（＝積分の考え方）。そうすると飛行機全体にかかる気圧がわかり、安全に飛べるのかどうかを分析することができます。

飛行機が安全に空を飛べるのは、微分積分のおかげなのです。