なぜ外れ値の取り扱いに気をつけなければならないのだろうか。それは外れ値がデータの要約に対して影響を与える可能性があるからだ。
例として、外れ値を含む場合と含まない場合の平均値を見てみよう。以下にサンプルデータを示す。データ①に対して外れ値として100を追加したものがデータ②である。
8、11、12、13、13、13、13、13、14、15、18
平均値:13
中央値:13
8、11、12、13、13、13、13、13、14、15、18、100
平均値:20.25
中央値:13
データ①の平均値は13、データ②の平均値は20.25で外れ値の存在により平均値が変化することがわかる。
また外れ値は相関係数にも与える。相関係数は2つのデータ間の関係性の強さを示す指標である。以下のサンプルを用いて相関係数を算出(エクセルのCORREL関数を使うと簡単)すると、外れ値を含まないデータでは0.01と低くなり、外れ値を含むデータでは相関係数0.98と高い。
●外れ値なし
| x | 8 | 11 | 12 | 13 | 13 | 13 | 13 | 13 | 14 | 15 | 18 |
| y | 22 | 20 | 29 | 27 | 25 | 29 | 21 | 29 | 28 | 21 | 22 |
※相関係数:0.01
●外れ値(x=100, y=106)あり
| x | 8 | 11 | 12 | 13 | 13 | 13 | 13 | 13 | 14 | 15 | 18 | 100 |
| y | 22 | 20 | 29 | 27 | 25 | 29 | 21 | 29 | 28 | 21 | 22 | 106 |
※相関係数:0.98
また、このサンプルを用いて作った散布図を見てほしい。
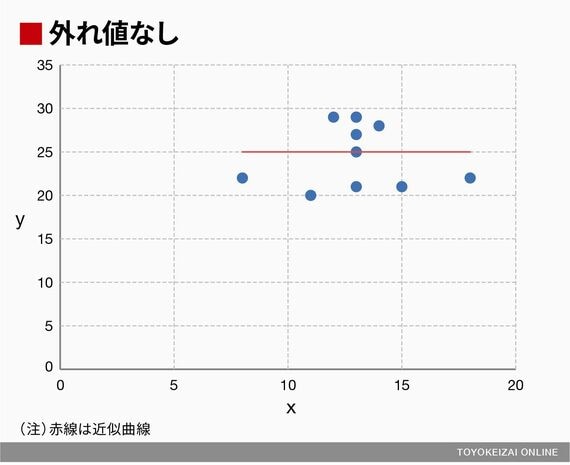
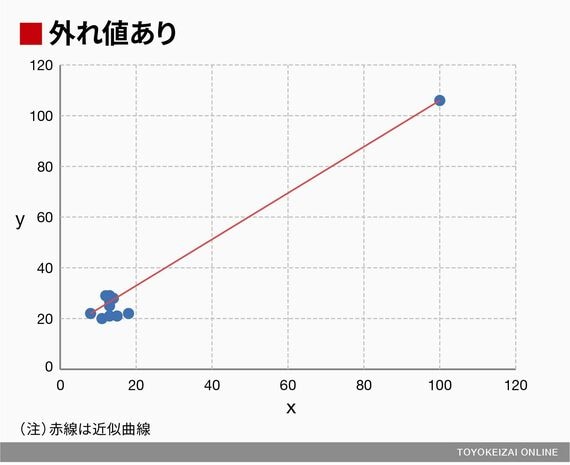
散布図を見てみると、外れ値なしのデータには相関関係がないのに、外れ値ありのデータでは、外れ値(x=100, y=106)に引きずられて相関係数が高く(相関関係が強く)なっているのがわかる。
ここでは外れ値が相関係数を引き上げる例を示したが、外れ値により相関係数が低くなる場合もある。このように相関係数は外れ値の影響を受けて数値が大きく変化する。
中央値は外れ値の影響を受けにくい
相関係数や平均値のように外れ値の影響を受けやすい指標がある一方で、影響を受けにくい指標もある。その代表例が中央値だ。前出のデータ①と②の中央値からわかるように、外れ値の有無で中央値は大きく変化しない。このような外れ値などの影響を受けにくいことを頑健と呼ぶ。
外れ値を含むデータを正しく読み解くためには外れ値を考慮した頑健な指標選びも重要である。
ここで挙げた例では外れ値の見分けがつきやすかったが、実データでは通常の数値と外れ値の境界が曖昧な場合が多い。ではどのようにして外れ値を探すのだろうか。大きく乖離したデータを外れ値というがその大きさはいかほどなのだろうか。































無料会員登録はこちら
ログインはこちら