｢視野が広い人｣だけが一瞬で解ける図形の超難問 東大生は数学で｢俯瞰して見る力｣を鍛えている

「接する」というのは、交わるわけでもないし、交わらないわけでもない、スレスレで1点だけでくっついている状態のことです。1つ例を挙げるのなら、こんな感じですね。

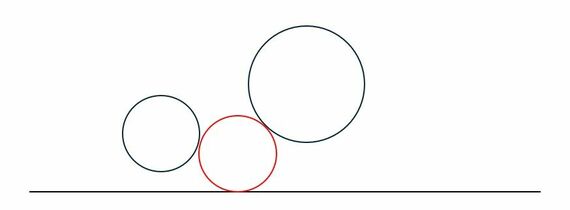
赤い丸が、線と2つの円に接している形になっています。「こういう円を何個書けるのか」というのがこの問題です。

「内側」「外側」で分けて考える

みなさんは、どれくらいの円を描くことができるでしょうか？ この問題は、2つまではすぐに思いつきます。先ほどの赤円は外側で両円と接している円でした。そしてそれに対して、内側で両円と接する円があります。

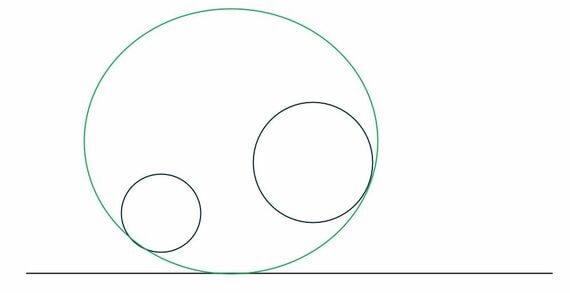
このような、緑の円ですね。

そして、同じように考えれば、もう2つ円を考えることができます。先ほどが「内側と内側」「外側と外側」という関係でしたから、「内側と外側で接する円があるのではないか？」と想像することができます。

そうしてよく考えると、内側と外側で接する円が2つあることに気づけると思います。これを考えると、次のような4つの円が考えられるでしょう。

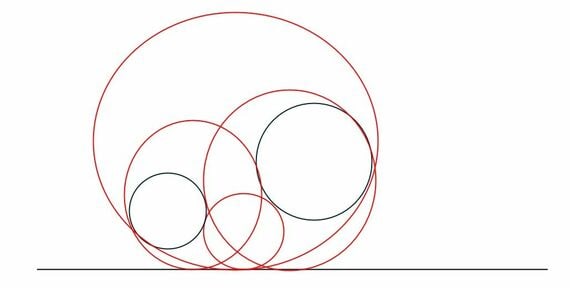
この4つの円で終わりなのではないか、と考える人も多いでしょう。でも実はこの問題、さらに4つ、追加で接する円があります。さて、どこにあると思いますか？