意外に解ける｢東大入試｣が思考力の訓練に使える ｢日常生活の1コマ｣をテーマにした問題が少なくない

実は、難しい計算はまったく必要なく、表を使って考えると、とてもわかりやすくなります。今回の場合、以下のようになります。

大型タクシー2台と小型タクシー3台の走行距離と運賃

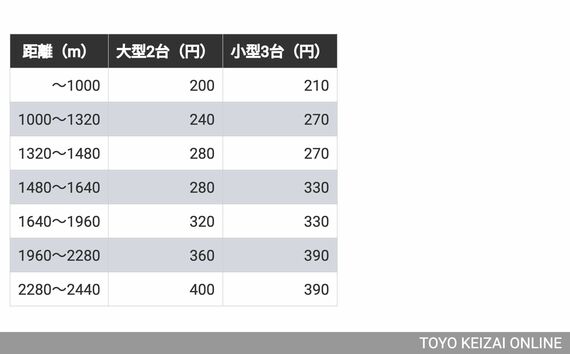
※外部配信先では表を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください

大型のタクシーと小型のタクシーで、料金が変わる距離のタイミングは異なるため、どちらも反映させています。料金を比較して小型のタクシー3台のほうが安くなるところは、1320～1480mと2280～2440mです。

大型2台、小型3台のどちらの場合でも、960mごとに120円ずつ料金が上がっていくため、2440m以上の移動距離となった場合も同じような料金の推移になることがわかります。

よって、この問題の答えは、

というかなり限られた条件になります。この条件下では、大型のタクシーを使うほうが得になる区間が大きいのです。数学の能力を鍛えることで、こうした日常の判断がより正確にできるようになるメリットがあります。

水道料金も東大入試で出題されている

多くの家庭が月ごとで払っている水道料金。毎月少しずつ料金が違うのを見て、「どういう仕組みで料金が算出されているんだろう？」と気になったことがある人もいるでしょう。実はこの水道料金も、東京大学では入試問題として出題されています。

この問題のポイントは、水道料金には「基本料金」という概念があることです。もしこれがなければ、使用した水の量に対して単純に水道料金をかけ算すればいいのですが、この基本料金があるため計算が複雑になっています。