｢御上先生｣あえて"間違った板書"をする深い理由 板書のミスを見つけてもらうことで得る学び

通常であれば、授業では問題の「答え」を先生が板書し、それを生徒が書き写すというスタイルが取られますよね。

わざと「間違い」を入れる

しかしこの授業では、わざと「間違い」を入れているわけです。そんなことをしたら間違った答えを生徒が学んでしまうんじゃないか、と思ってしまいますが、「この中には間違いが含まれている」とあらかじめ言っておくことで、生徒自身に「どこが間違っているか」を考えてもらう、「間違え探し」のような授業を行ったわけですね。

※外部配信先では画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください

（写真：東大カルペ・ディエム提供）

実際にこのシーン、よく見れば白字の解答には計算ミスがあったり、論理のミスなどが散見されるものになっています。

例えば、数列の和を取るところで、覚えている公式をそのまま使ってしまって間違えるという典型的な計算ミスをしています。数学ができる人からすれば、こんなのすぐわかるだろ！と思われるかもしれませんが、授業だとこういったミスは見過ごされがちです。

このようなミスを回避するには、例えば小さなnに具体的な値を入れて計算のチェックをするのがオススメです。例えば今回の例だと、実際にn=3などを入れてみると、間違いがわかります。

（図：筆者作成）

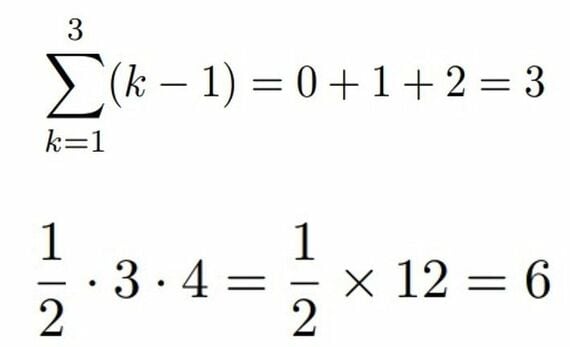
図のように、明らかに間違っているとわかるのです。一般のnで合っているかわからないような式に、具体的な数字を代入して確認を行うというのは、受験本番で失点を避けるための必須のテクニックです。

他にも、このシーンでは、受験生の解答で減点されがちな「必要条件・十分条件」の同値性のミスを再現しています。

この箇所も、論証の大筋は間違っていませんが、この書き方だと「証明の十分性しか示していない」と採点者に思われかねません。

（写真：東大カルペ・ディエム提供）

（写真：東大カルペ・ディエム提供）

よく受験数学の指導の際、同値記号（⇔）の多用は避けるべきと言われますが、問題で「必要十分条件を求めよ」と明示されている場面に限っては、自分がわかっていることをきちんと伝えるために、同値記号を用いて解答を書くのがよいと言われています。

答えの数字があっているからといって、書き方で減点される可能性があるということを意識するためには、このように「大学受験であれば減点されるポイント」、そして「そもそも出題者は、この問題を通じて、受験生のどんな力を測りたいのか」ということを自分で見抜けるようにしなければならないわけですね。