中学生でも解ける｢素数はほぼ6の倍数±1｣の証明 ただし｢2と3｣は除く。あなたは解けますか？

これ、数が大きくなっても基本的には変わりません。こちらをご覧ください。こちらは、1001〜1050までを表にしたものです。

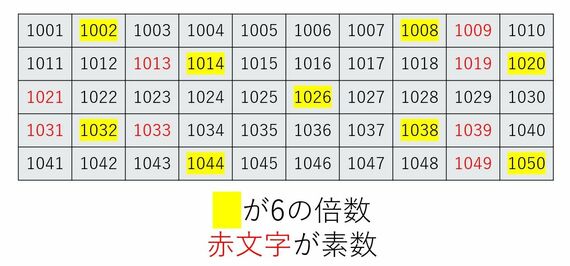
やっぱりこちらも、「6の倍数」の隣が素数になっています。というか実は、「2、3」以外の素数は、すべて「6の倍数」の隣にあるのです。

「2、3」以外の素数は、「6の倍数±1」――これって不思議だと思いませんか？「6の倍数＋2」「6の倍数＋3」とかの数があってもおかしくないじゃないか、と思いますよね？

数を「一般化」して確かめていく

さて、これについて考えるときには、「一般化」が必要です。数学では、「〇〇を××とおく」という表現が出てきます。「点Pの座標を（x , y）とおく」とか、「求める確率を『αn』とおく」とかですね。これと同じように、6の倍数も記号で表してみましょう。すると、こんなふうになります。

こうすると、nがどんな整数だったとしても、「6n」は絶対に6の倍数になります。そして、6nを基準に考えると、6以上のすべての整数は下のいずれかに当てはまります。

例えば19は「6×3＋1」ですから、「6n＋1」の仲間ですね。51は「6×8＋3」ですから、「6n＋3」の仲間です。66は「6×10＋6」ですが、この場合は「6×11」と定義できますから、6nと表現できます。このように、6以上の整数は「6nにいくつプラスするか」で表現することができるわけです。

そう考えたときに、素数になる可能性があるのは、どれでしょうか？

まず、「6n」はダメですね。6の倍数ですから、素数になるはずはありません。

「6n＋2」はどうでしょう？ 8とか14とかですが、これは2の倍数になってしまいます。当たり前ですが、6は2で割れて、2も2で割れます。ですから「6n+2」は、2の倍数、偶数なのです。もっと数学的に説明すると、「6n＋2＝2（3n＋1）」と、2で括れてしまいますから、2の倍数になるわけです。