中学生でも解ける｢素数はほぼ6の倍数±1｣の証明 ただし｢2と3｣は除く。あなたは解けますか？

素数とは「1」と「その数」でしか割り切れない数のことです。

例えば「5」という数は、1と5でしか割れませんよね。「13」という数も、1と13でしか割れません。このように、「1」と「その数」でしか割ることのできない数のことを素数と言います。

素数は「法則性なく」存在している

素数は、ほとんど法則性なく存在していると言われています。

素数を小さいほうから並べると、「2、3、5、7、11、13、17、19、23、29……」となるわけですが、どうでしょう？ この並びに、法則性なんてなさそうですよね。

「2の倍数」とかだったら、「2、4、6、8、10、12、14、16、18、20、22……」という感じで、「1桁目が2の倍数」という法則性がありますが、素数にはほとんど法則性がないのです。

でも、ちょっとだけ言えることもあります。それが、「2と3以外の素数は、6の倍数±1」というものです。

例えば「6」と、それを±1をした「5、7」を考えてみましょう。「5」と「7」はどちらも素数ですよね。「12」は「6×2」ですから6の倍数で、それを ±1をした「11、13」はどちらも素数です。「18」も「6×3」ですから6の倍数で、それを ±1をした「17、19」も、どちらも素数です。

1～50までの数を確認してみましょう。表を作ったのでご覧ください。

（外部配信先では記事中の図表などの画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

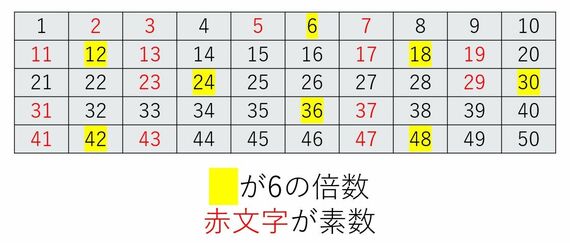
最初の「2、3」以外の素数は、すべて「6の倍数」の隣、つまり±1をした数になっていることがわかるでしょうか？ もちろん、「24」の隣の「25」とか、「36」の隣の「35」とか、素数になっていないものもありますが、素数は必ず「6の倍数」の隣にあるのはわかりますよね。