知ると便利｢膨大なデータから潜在顧客見抜く｣技 データを類似性で分類する｢クラスター分析｣

クラスター分析手法は大きく「階層クラスター分析」「非階層クラスター分析」の2つに大別され、いずれもRやPythonなどのソフトウェアを使って実行することができる。

まず階層クラスター分析は、各データ間の距離を基にして近いデータ同士を段階的にまとめる形でクラスターを作成する手法である。各クラスター間の距離の計算方法には、ウォード法や重心法などがある。

図2を例にすると、まず点Dと点F、点Hと点I、点Aと点Cの順に近い2点がまとめられる。次いで点G～I、点D～F、点A～Cの順に3点ずつまとめられ、最後に大きく点D～Iがまとめられる。

図2：階層クラスターの分析イメージ

図は筆者作成

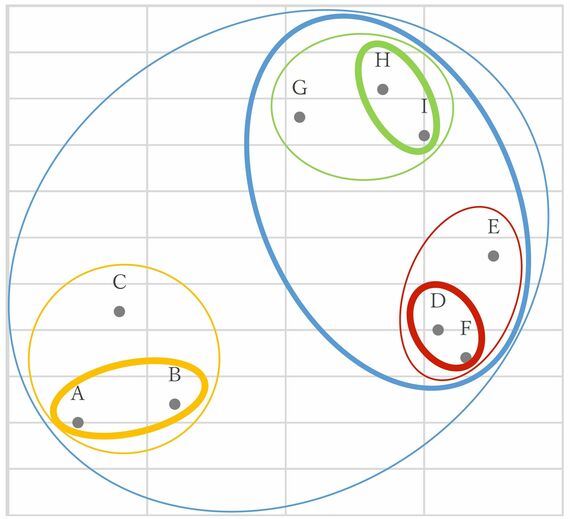
分類過程がこのように段階的になり、まとめられ方を表す図3の樹形図（デンドログラム）が分析結果として作成される。

図3：分析結果として作成された樹形図（デンドログラム）

図は筆者作成

樹形図の横のつながりはまとめられた順番を、縦の長さ（高さ）はクラスター間の距離を表す。枝が長いほど距離が遠く、図3の例では点A～Cクラスターと点D～Iクラスター間の距離が最も遠い。

階層クラスター分析の長所と短所

階層クラスター分析には、後述の非階層クラスター分析と違って事前にいくつクラスターを作成するか決める必要がなく、分類結果の樹形図を見て目的に応じて自由にクラスターを分けられるという長所がある。

図2、3の例でいえば、点A、Bを1クラスターとしても、点A、B、Cを1クラスターとしてもよい。樹形図が直感的にわかりやすいため、容易に分析に役立てられる。その一方で、データ数が多すぎると統計ソフト内の計算や分析後の解釈が困難になるという短所もある。

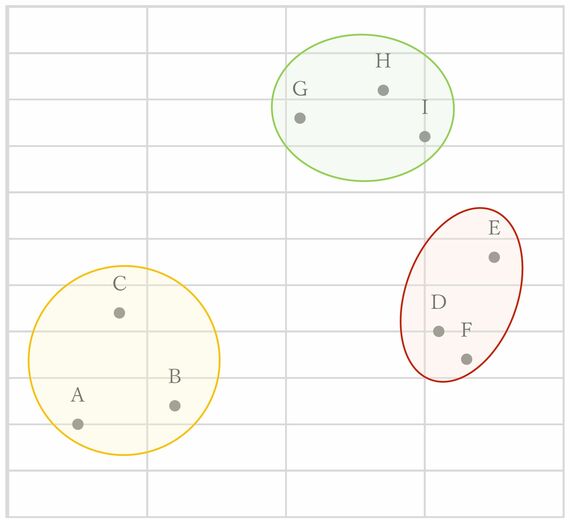
対する非階層クラスター分析は、いくつのクラスターに分割するかをあらかじめ分析者が決め、類似度が高いデータ同士が同じクラスターになるように、全体を決めた数に分割する手法である。代表的な手法としては、k-means法が挙げられる。図4は、クラスター数3の設定でk-means法を行った際のイメージである。

図4:クラスター数3で非階層クラスター分析(k-means法)を行った際のイメージ

図は筆者作成