数学嫌いに伝えたい｢sin｣｢cos｣が社会で役立つ訳 実生活のさまざまなところで使われている

夕方あるいは明け方、太陽が傾いているとき、タレスは太陽に背を向けて立ち、自分の影の長さが自分の身長とちょうど同じになるまで待ちました。影と身長が同じ長さということは、図1に示したような直角二等辺三角形ができたということです。

●図1

出所：『教養としての「数学Ⅰ・A」』

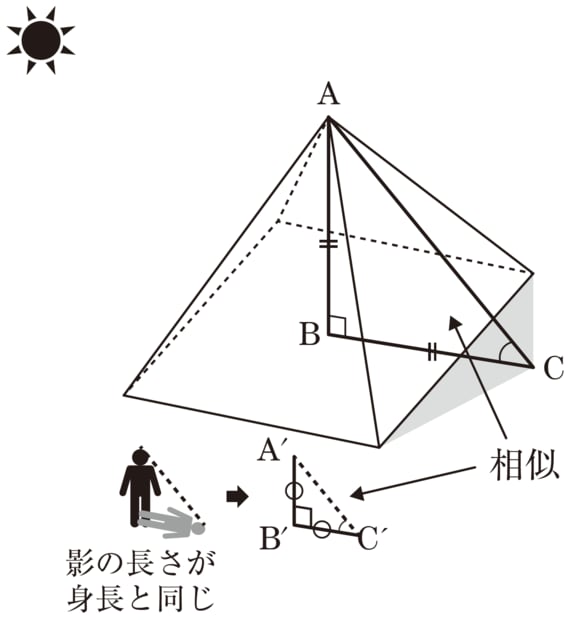
（外部配信先では図や画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

そして同じときに、ピラミッドの影の長さを測ります。ピラミッドのほうにも大きな直角二等辺三角形ができているので、ピラミッドの1辺の長さを測り、その半分を影の長さに足せば、ピラミッドの高さがわかるというわけです。

タレスは、自分と自分の影がつくる直角三角形と、ピラミッドとピラミッドの影がつくる直角三角形は相似であることを利用しました。現代の私たちからすれば誰か気づいてもよさそうなことですが、当時の人はこの発想に大いに驚いたそうです。

直角二等辺三角形に限らず、すべての直角三角形は直角以外の角度の1つが等しいとき、必ず相似になります。

人類が「角度」に興味を持ったきっかけ

そもそも人類が「角度」に興味を持つようになったきっかけは、夜空の星の位置を把握しようとしたからでした。古代では天動説、つまり地球は静止していて星々が地球の周りを回っているという説が信じられていました。天動説では、地球の外側には「天球」と呼ばれる巨大な球体があり、地球以外の星はこの天球上を移動すると考えます。

天球上を移動する星を研究するうちに、人々の興味の対象はやがて、円の中心角と弦（げん）の長さの関係へと移っていきました。古代ローマのプトレマイオスが2世紀にまとめた「弦の表」には半径60の円について、いろいろな中心角に対する弦の長さが細かく調べあげられています。実質的にはこれは、のちにいうところのsinの値を調べたのと同じことでした。

ちなみに、半径が「60」なのは、当時天文学では60進法が使われていたからです。

こうしてプトレマイオスは、最終的に天体の運動を説明する理論を構築していきます（もっとも、天動説に基づく彼の理論は地動説の登場によって否定されることになりますが）。