数学嫌いに伝えたい｢sin｣｢cos｣が社会で役立つ訳 実生活のさまざまなところで使われている

数学Ⅰで習う「三角比」、これは三角形の辺の比のことです。sin（サイン）、cos（コサイン）、tan（タンジェント）はどの辺とどの辺の比を表しているか、どれがどれだかわからなくならないよう、これを覚えるための有名なテクニックがあります。

それは図2に描いた方法です。

●図2

出所：『教養としての「数学Ⅰ・A」』

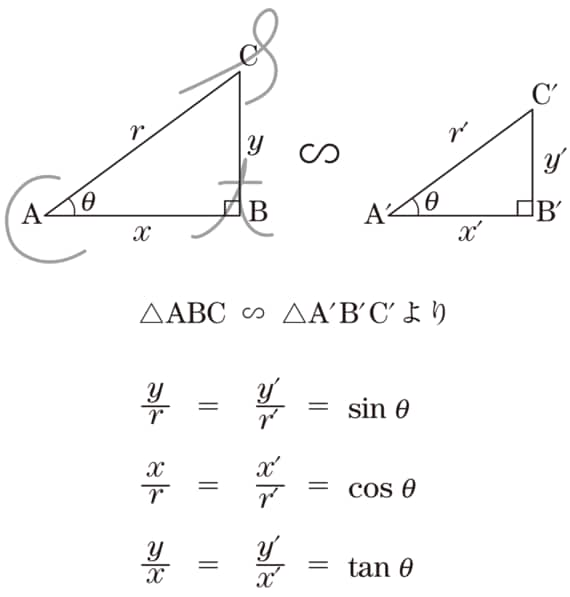
sinは＜斜辺＞分の＜高さ＞（つまりr分のy）だから筆記体の“s”、cosは＜斜辺＞分の＜横＞（つまりr分のx）だから“c”、tanは＜横＞分の＜高さ＞（つまりx分のy）だから小文字の“t”の字体でそれぞれ覚えるというやり方です。高校時代に習ったことを思い出したでしょうか。

もちろんこの覚え方が悪いとはいいませんが、もう少し本質的なことを理解しておいたほうが、後々応用が利きます。その方法を紹介しておくことにしましょう。

各辺がどういう関係か、パッと思い浮かぶようにする

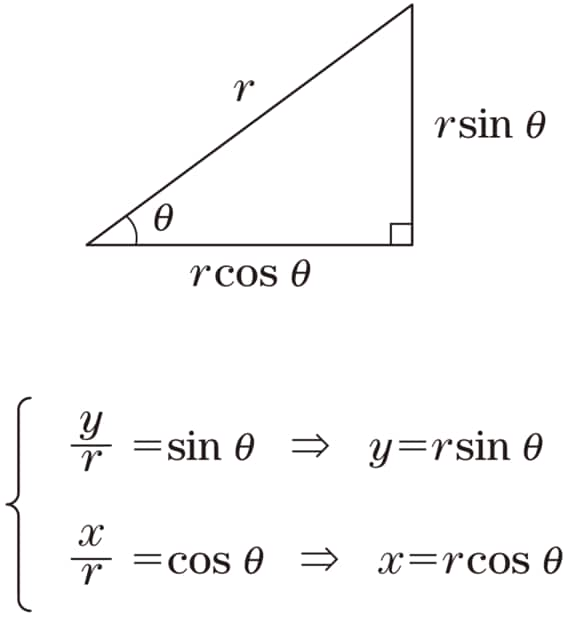
重要なことは、直角三角形を見たとき、各辺がどういう関係になっているのか、パッと思い浮かぶようにするということです。r分のyはsinθ、r分のxはcosθですから、これらを式変形すると（両辺にrをかけると）、y=r×sinθ、x=r×cosθということになります。

すなわち、斜辺の長さをrとした直角三角形において、横の長さはrcosθ、高さはrsinθと示せることになります。

三角比といわれたら、以下の図3が頭に浮かぶようにしてください。

●図3

出所：『教養としての「数学Ⅰ・A」』