数学嫌いに伝えたい｢sin｣｢cos｣が社会で役立つ訳 実生活のさまざまなところで使われている

次は、三角比の実用性を知るため、以下の例題をやってみましょう。

出所：『教養としての「数学Ⅰ・A」』

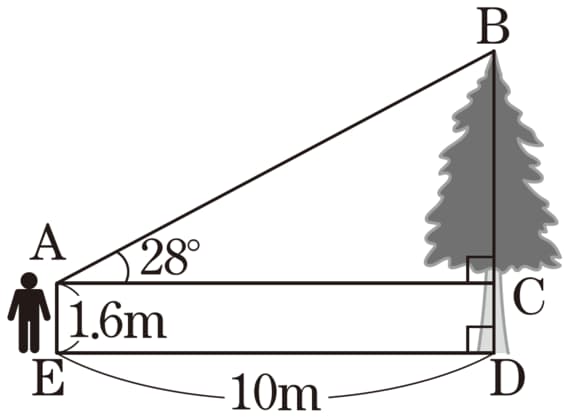
木までの距離と仰角（ぎょうかく）さえわかっていれば、実際に木の高さを測る必要はありません。

tanは＜横＞分の＜高さ＞でしたから、BC＜高さ＞は、木までの距離AC＜横＞10mに、tan28°をかければ得られます。tan28°の値は、関数電卓を使えばすぐに出てきます。

iPhoneをお持ちなら、電卓アプリを呼び出して本体を横にしてみてください。tan28°はだいたい0.5317だとわかります。

これに木までの距離10mをかけて、自分の目までの高さ1.6mを足せば、木の高さを測ることができます。

このように三角比を使って行う測量を「三角測量」といいます。タレスが行ったピラミッドの高さの測定も原初の三角測量といえるでしょう。

街中での測量や人工衛星の位置調査にも使われている

街中で、望遠鏡のような機器（測量器）を覗き込んでいる測量士を見かけたことがあるかもしれません。あのような測量器で測っているのは、角度です。途中に川があるなどの理由で、直接測ることが難しい高さや距離を三角測量で求めているのです。

『教養としての「数学I・A」』（NHK出版）。書影をクリックするとAmazonのサイトにジャンプします。

幾何学のことを英語ではgeometryといいますが、この言葉は「地」を表すgeoと、「測定」を表すmetriaからできています。もともと、測量をすることから幾何学は生まれてきたのですね。

人工衛星の位置を調べるのも、三角測量です。2つの恒星と、対象の人工衛星で三角形をつくり、角度を測って位置を割り出しています。

さらに、数学Ⅱになると三角比は、三角関数へ格上げされます。三角関数のグラフは同じ波形が繰り返し現れる周期関数になるのですが、それを使ってさまざまな物理現象を解析することができます。

もう「sin（サイン）やcos（コサイン）なんて社会で役に立たない」なんて発言はまったくナンセンス、ということはわかっていただけたのではないでしょうか。