データ見て｢60％と57％に差あり｣と思う人の盲点 ビジネスに役立つ｢統計数字｣の正しい見方

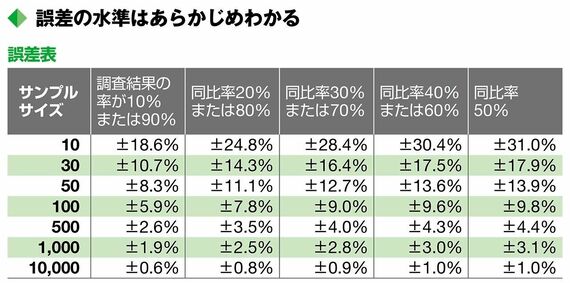
では、具体的に標本誤差はどのように計算されるのだろうか。実務では、図のような誤差表を使うと便利である。

（筆者作成）

（外部配信先では図表・グラフや画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

標本誤差は、サンプルサイズと調査結果の比率から計算することが可能である。

例えば、サンプルサイズが1000人で、調査結果の認知率が60%だったとする。このとき、実際に計算をしてみると、標本誤差は±3% （信頼度 95%）になる。すなわち、母集団における真の認知率は、60%の±3%すなわち57%～63%の範囲に収まると、解釈することができるのである。

偶然なのか、意味のある差なのかを判断する方法

このような前提を理解したうえで、冒頭に挙げた2つの調査結果を比較する例を考えてみたい。

関東は60%、関西は57%という結果であったが、それぞれの結果には標本誤差が含まれている。では、私たちはどのようにして、この2つの結果の差を捉えていけばいいのだろうか。こうしたときに役立つのが、「統計的仮説検定」の考え方である。

統計的仮説検定を用いると、先の例で言えば、2つの調査結果の差が、偶然による差なのか、それとも偶然ではなく確かに意味のある差（有意差）なのかを判断することができる。この記事では、統計的仮説検定について具体的に説明していきたい。

ただし、初めて学ぶ人には、統計的仮説検定の考え方は少しなじみにくさがある。理解を深めていくために、まずはそのプロセスを説明したい。

統計的仮説検定は、大きく分けて3つのステップで進められる。