データ見て｢60％と57％に差あり｣と思う人の盲点 ビジネスに役立つ｢統計数字｣の正しい見方

ステップ1は、帰無仮説の設定である。帰無仮説とは、差がない、関係がない等の無（＝0）を意味する仮説である。例えば、「関東と関西の認知率に差があるか」を検定するには、「両者の認知率が等しい（差が0である）」という帰無仮説を設定することが必要になる。

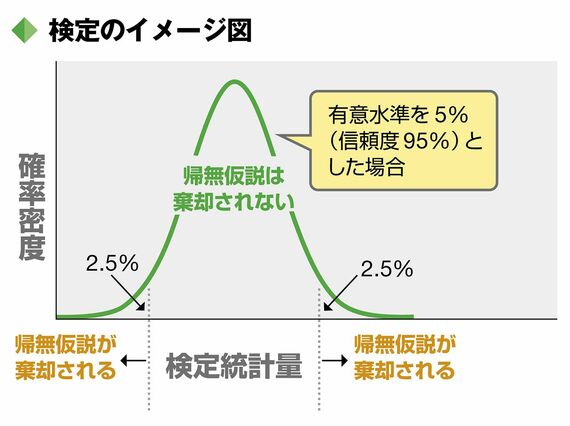
また、分析者はあらかじめ「有意水準」と呼ばれる帰無仮説が間違っていると判断する（棄却する）基準を設定しておく。通常、有意水準には、1%、5%、10%が使われる。5%に設定した場合、100回中5回以下の確率で生じる現象については、めったにおきない非常にまれなことがおきたと判断する基準になる。

ステップ2は検定統計量の計算である。検定統計量は、本記事の例では「両者の認知率が等しいはずなのに実際のデータでは差が出る」事象が“どのくらいまれか”を示す値である。検定統計量にはいくつかの種類があり、用いる検定方法に応じて使い分けられる。

ステップ3は、帰無仮説の棄却である。検定統計量を計算した結果を有意水準と照らす。その結果、めったに起きないことが起きた（偶然にしてはおかしい）のであれば、そもそも帰無仮説が誤りだと棄却し、「関東と関西の認知率には有意差がある」と判断する（対立仮説を採択）。

なぜ統計的仮説検定が初学者になじみにくいかというと、「①帰無仮説を②棄却する」という二重否定のまわりくどい論理を使っているからだ。

関東と関西の認知率には差があるという仮説をもっとシンプルに検証できないのかと思う方もいるかもしれない。しかし、実際には、仮説の正しさを証明するのは難しい。一方、仮説が正しくないことを証明することは反例を1つあげればいいので簡単である。

世の中のすべてのカラスが黒いと証明する方法

この問題を考える時によく挙げられるのが、黒いカラスの例である。今、私たちは「世の中のすべてのカラスが黒いこと」を証明したいとする。

すべてのカラスが黒いことを証明するには、この世のすべてのカラスを観察して黒いことを確かめる必要がある。しかし、すべてのカラスは黒いことが間違っていることを示すには、1匹でも白いカラスを見つければよい。

同様に、本記事の仮説検定の例で言えば、2つの結果に差がないことが間違っていることを示すためには、差がある例を挙げればいい。両者の認知率が等しいはずなのに実際のデータでは差がある、それは偶然にしてはおかしいので、そもそも仮説が正しくないと判断するのである。

こういった考え方は、一般的にはなじみにくいが、科学的な実証においてはよく使われるものなので、ぜひ覚えておきたいものである。