統計的仮説検定の方法を理解していくために、実際の数値に基づいた事例を考えていきたい。ここでは、ビジネスでよく使う、「異なる集団間における比率の差の検定」を例として、実際に検定を行ってみよう。
まず、次のようなデータが得られたとしよう。関東ではサンプルサイズが200人（n1）で認知率が60%（p1）、関西では300人（n2）で57%（p2）であった。ここでは、「関東と関西の認知率に差があるか」を検定したいため、先ほど述べたように「両者の認知率が等しい」という帰無仮説をまず設定する。また、有意水準は5%を設定する。
| 関東 | 関西 | |
| サンプルサイズ | 200（n1） | 300（n2） |
| 認知者 | 120 | 171 |
| 認知率 | 60％（p1） | 57％（p2） |
次に、検定統計量を計算する。異なる集団間における比率の差の検定の場合、検定統計量は、以下のように表すことができる。
●検定統計量
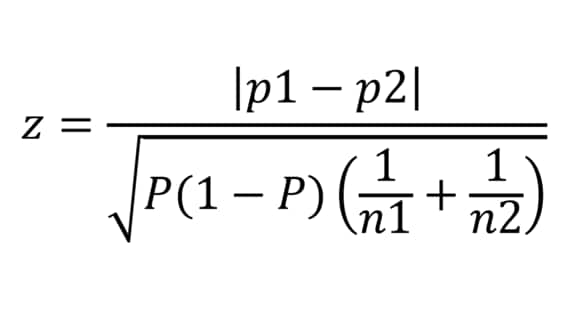
●加重平均
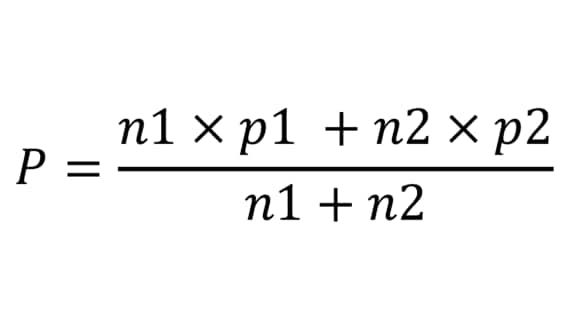
式だと難しく感じられる読者の方もいるかもしれないので、実際の数値例も見ていこう。まず、サンプルサイズと認知率のそれぞれの値から加重平均を計算する。ここで、加重平均の分子は認知者の和に等しい。
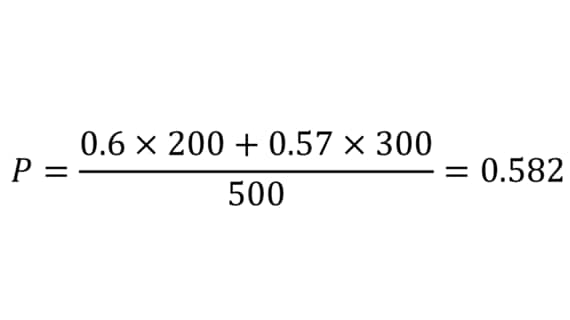
次に、ぞれぞれの値を使いながら、検定統計量を計算する。
計算の結果、検定統計量は0.666であった。今回設定した有意水準5%では、1.96以上であれば、有意差ありと判定される。したがって、今回の事例では、帰無仮説は棄却されず、「関東と関西の認知率に（有意な）差があるとはいえない」と結論づけられる。
では、関東では認知率が55%、関西では30%という以下の数表の例ではどうだろうか？
| 関東 | 関西 | |
| サンプルサイズ | 200（n1） | 300（n2） |
| 認知者 | 110 | 90 |
| 認知率 | 55％（p1） | 30％（p2） |
同様に計算すると、検定統計量は5.59であった。これは、有意水準5%のとき検定統計量zの基準である1.96以上であるため、有意差ありと判定される。したがって、この事例では、帰無仮説が棄却され、「関東と関西の認知率に（有意な）差がある」ことを示すことができた。
●加重平均
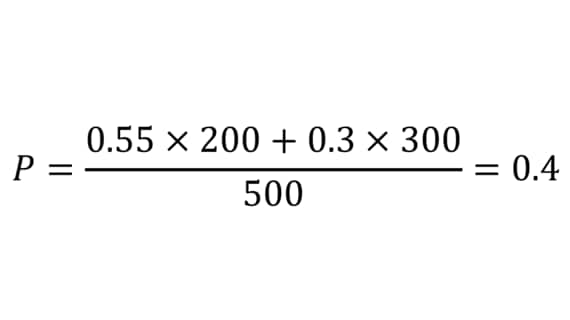
●検定統計量
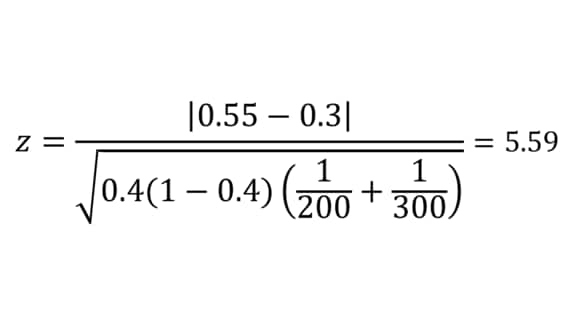
最後に、検定を行うときに気をつけておきたいポイントを挙げておく。
「有意差がある」というのは「差が大きい」ことを意味しているわけではないことに注意をしておきたい。同じ差でも、サンプルサイズが大きければ有意になり、小さければ有意にならないことがある。仮に10％の差があっても、10人の調査と1000人の調査では、検定の結果は変わる。
したがって、統計的仮説検定は、その結果に「差があることが確からしい」ことを、得られたサンプルサイズの条件下で確認するためのものであることを理解しておきたい。
ログインはこちら