｢鉛筆1本＋傘1本＝2本｣という足し算は正しいか 小1レベルの足し算も教えるのは本当に難しい

ところが、教え方の「裏技」としていきなりこんな計算を持ち出す人もいるようです。

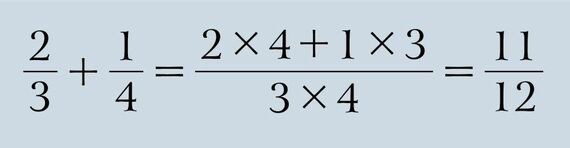
「2/3と1/4を足すときは、2つの分母同士を掛けた3×4＝12が答えの分母となって、1つ目の分数の分子に2つ目の分母を掛けた2×4＝8と、2つ目の分子に1つ目の分母を掛けた1×3＝3、この2つの値を足した8+3＝11が答えの分子になる。だから答えは11/12。このやり方は他の足し算でも使えるから、覚えておいて」

こうやればできるよ、覚えておけばいいよ、と教える人がいるのではないでしょうか。昔は学校の授業で何かやったかもしれないがそんなのは忘れた、でもこの方法だけ覚えておけば解ける、テストで「○」がもらえればそれでいいじゃないか、と。

小学校ぐらいのことなら自分でも教えられると思っている親御さんによく見受けられます。

でもそういう人は決まって「高校の微積とかわからないけれど」と言います。ここで実はかなり大切なことが忘れられています。子どもたちが幸福を感じられるのは単にテストで「○」がもらえたからだけではありません。数の計算という複雑怪奇な世界を認識できてよかった、いやということなのです。自分自身ではそれが上手くいったかどうかわからない。そういう状況において他者から評価を受けることでその達成が確信できるのです。

よくわからないけれど「○」をもらったからいいや、というのは外から見た表象的なものであり、学んだ本人の感覚ではありません。

「解き方」だけを詰め込み数学の世界が分断される

子どもはみんな冒険者です。どんどん新しい世界へ向かっていこうとします。もちろん内なる世界へ向かっていく子どももいますが、自分の世界を拡げ、また深めようとします。そこでは単に「○」がもらえるという報酬だけでは長続きしないのです。

しかも計算方法を丸暗記しても結局忘れてしまう。意味づけをすることが長期記憶につながるというのが心理学で言われていることです。

裏を返せば解法丸暗記では、ある程度までは解けたとしても限界が来ます。

問題数をこなすことで「ああ、このやり方か」とパターンに当てはめることはできます。しかし、そのパターンから外れたものには歯が立たなくなるのです。