｢鉛筆1本＋傘1本＝2本｣という足し算は正しいか 小1レベルの足し算も教えるのは本当に難しい

数学の研究をしているというと「ああ、なぜ1＋1＝2になるのか研究しているんですね」と言う人が必ず出てきます。それで一本取ったつもりになるのだろうけれど、専門家はその程度のことでは怯みません。それには専門的にきちんとした答えが用意されています。結論から言うと「そもそもそういう世界であるとして作られているから」。多少叱られることを覚悟で言うならば、「自然数（個数や順番を数えるための数、1、2、3、…のこと）の定義に含まれる」としてもいいと思います。ここで「定義」とは用語や概念を規定する文であるとしておきます。

そもそも1とは何なのでしょう。2とは何か、＋とは何か。

厳密な議論をしようとすると数学者の間でもいろいろな立場があるのでここでは深入りしませんが、少なくともこの小学校1年生の疑問は実はかなり本質的で、「数とは」「数えるとは」というあたりまで踏み込んだ話になるのです。この場合で言えば、「チューリップは何本でしょう」「デパートで売っている物は何本でしょう」と言えば話がまとまります。個人的なことですが、教員免許更新講習においては、小学校の先生方に毎年この話をしていました。

「〇をもらえるよ」と言う大人が一番危うい

また別の問題を考えてみましょう。

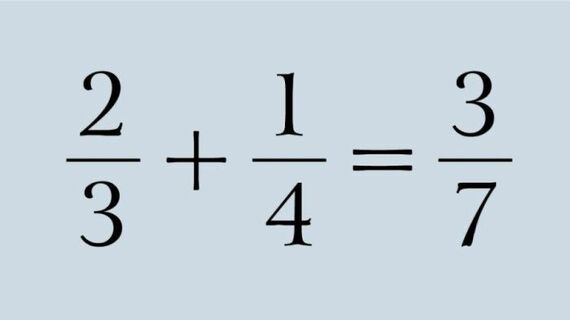
「2/3と1/4を足す」という問題は、「分母同士の3と4を足す、さらに分子同士の2と1を足して、3/7」となる。

どう思われますか。これは「間違っている」のでしょうか。

たしかに、分数の計算としては不正解です。しかし、「1+1=2」という世界で学んで来た子どもにとっては、「なぜ？」と思うのもまた自然なことです。

この場合は、分母を12に通分することで、はじめて分子を普通に足し算することができます。分数の世界をしっかり知ると、そこに1+1=2の世界とのつながりがみえてくるわけです。