市場とかけ離れる、日銀の物価動向判断 フォワードレートが証明する「2％物価目標達成」の難しさ

1年債利回りは2年後でも0.17％

以下では、「フォワードレート」を計算する。「n年後のm年債のフォワードレート」とは、「n年後にm年債を買う（あるいは売る）」と現時点で先物契約をした場合の利回りである。先物契約は、n年後の経済状況がどのようになっていようとも履行しなければならない。つまり、これはリスクのない取引の金利だ。

すべてのnやmに対応した先物取引が現実に存在しているわけではないが、イールドカーブに含まれている情報を用いれば、以下のように計算することができる。これが「インプライド・フォワードレート」だ。

現時点の2年国債利回りは0.11％であり、3年国債利回りは0.13％である（利率は年率表示、以下同様）。ここで2年後の1年債のフォワードレートをx％としよう。

現在から2年間を2年債で運用し、その後1年間を1年債で運用する。ただし、その利回りは、現時点で先物契約をして、x％と確定しておくことにする。この場合、現時点で1投資すると、3年後には1.00112×（1＋x／100）となる。

他方、3年債で運用した場合には、1.00133となる。両者はリスクのない運用だから、3年後の資産額は同一にならなければならない。この関係から、xを0.17と計算することができる。

この値は、現在の3年債の利回りより高いことに注意が必要だ。つまり、今後の3年間において、最初の2年間はあまりリスクがないが、その後にリスクが大きくなると考えられているわけだ。

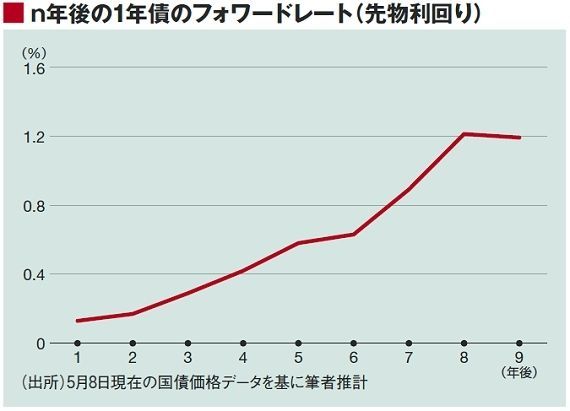
最近時点の日本国債の利回りのデータを用いて、n＝1～9について1年債のフォワードレートを計算すると、図に示すとおりとなる。

時間の経過とともにレートが徐々に上がっている。これは将来になるほどインフレ期待が高まるのを示していると解釈することもできる。ただし、2年後でも0.17％であるから、その時点のインフレ率が2％になっていることはありえない。つまり、マーケットは、2％目標はとても実現できないと判断していることになる（この点は、以下で詳しく述べる）。したがって、『物価展望レポート』の見通しは、市場の見通しとかけ離れているわけだ。

なお、フォワードレートは、9年後くらいからは一定値に収束する。これは、経済の長期的均衡を示していると解釈できる。