数学的に解説！お見合いパーティーで「1番好きな人」とマッチングできない理由　なぜアルゴリズムは「第2希望が最適解」と導くのか

実際に、不安定マッチングの例を1つ示そう。

（画像：『教養としての数学史』より）

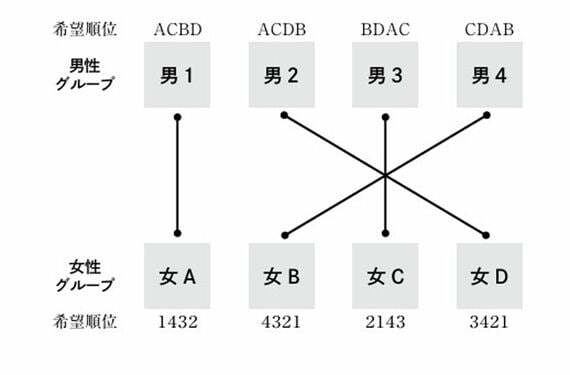
男性3は女性Cとペアになっているが、女性C以外の女性とペアになれるチャンスがあるならそちらを選びたい状況だ。女性Dは男性2とペアになっているが、こちらも男性3か男性4とペアになれるチャンスがあるならそちらを選ぶ。

したがって、次のように駆け落ちペアが誕生し、当初のマッチングは不安定であることがわかった。

（画像：『教養としての数学史』より）

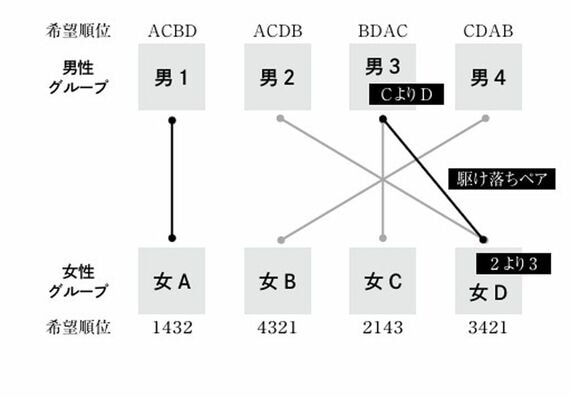
安定マッチングはどうか。

（画像：『教養としての数学史』より）

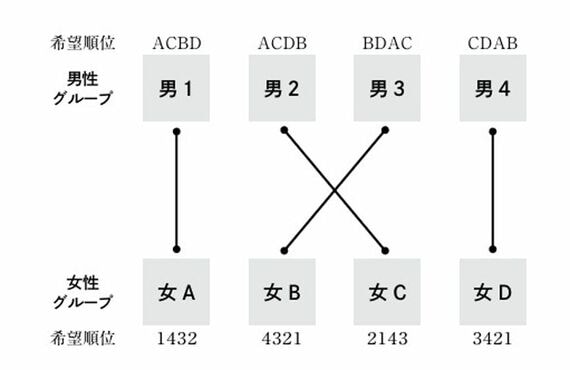
女性Bや女性Dは第2希望の男性とペアになっている。

しかし、女性Bが第1希望の男性4に告白をしても、男性4は女性Bより好んでいる女性Dとペアであるため現状維持を選ぶだろう。

同様の理由で女性Dも男性3に告白しても断られてしまうため、駆け落ちペアが成立せず、女性Cや女性Dにとっては不本意ながらも安定マッチングの状態なのだ。

「全員がそこそこ満足する」安定マッチングのつくりかた

各人の思いが交錯するマッチングの場において、安定マッチングをどう作ればいいのか。その方法こそ、ゲイルとシャープレーが考えた「ゲイル・シャープレーアルゴリズム」である。