つるかめ算､学んでも無駄と思う大人が知らぬ本質 実はさまざまな｢ものの見方｣がつまっている

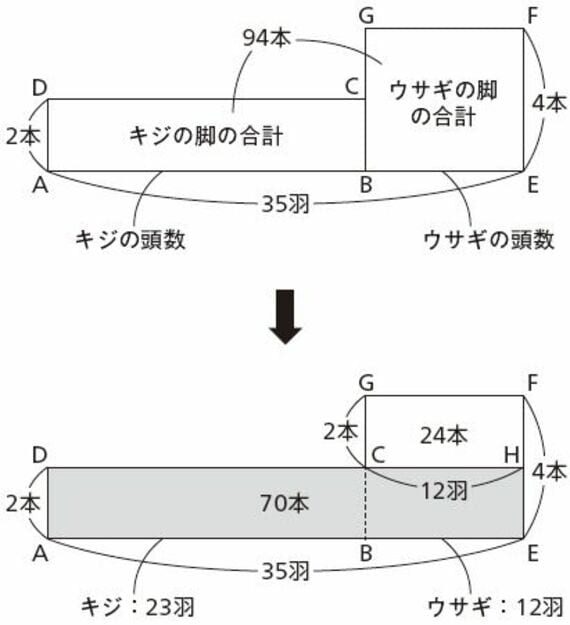
以下の図でABの長さはキジの頭数、BEの長さはウサギの頭数を表すことにすると、左の長方形ABCDの面積はキジの脚の合計、右の長方形BEFGの面積はウサギの脚の合計を表すことになります。

キジとウサギの脚の合計が94本であることは、この2つの長方形の面積の合計が94であることを意味します。

（出所：『おとなのための「中学受験算数」 問題解決力を最速で身につける』）

※外部配信先では図を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください

さて、ここでDCをCの側に延長して長方形DAEHをつくると、この長方形の面積が70になることから、右上の長方形CHFGの面積は24であることがわかります。ここでCGの長さはEFとADの差ですから「2」ですね。よって、CHの長さすなわちウサギの頭数は12羽とわかります。全部で35羽ですからキジは23羽と求まるわけです。

つるかめ算を長方形を使って図解する経験は、「速さ×時間＝距離」とか「濃度×食塩水の重さ＝食塩の重さ」とか「平均×個数＝総数」のような掛け算で表される量（2次の量）はいつも、面積を使って図解できるという学びにつながります。

特殊算の「うまい工夫」の中に多くの気づきがある

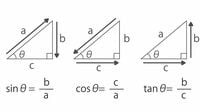
古代ギリシャのピタゴラスは、いわゆる三平方の定理（直角三角形で、直角をはさむ2辺の長さをaとb、斜辺の長さをcとすると、a²＋b²＝c²が成立するという定理）を証明する際、面積を使いました。三平方の定理もまた2次の量についての式だからです。

『大人のための「中学受験算数」 問題解決力を最速で身につける』（NHK出版新書）。書影をクリックするとアマゾンのサイトにジャンプします

つるかめ算は、特殊算の中でもとくに学ぶべきところが多いものではありますが、他の特殊算にも同じような「うまい工夫」があり、そこには方程式を使って機械的に解いてしまうことからは見えてこないさまざまな気づきがあります。

もちろん、どんな問題でも型通りに解けてしまう方程式の力は偉大です。未知なる問題を演えき的に解くための準備として包括的な方程式の解法を学んでおくことは非常に有意義です。

しかし、それを学ぶのは中学生になってからでよいと私は考えます。ものの見方のバリエーションを増やす経験として、また、問題解決のための数学的な発想を磨く機会として、頭の柔らかい小学生のうちに特殊算に取り組むことは決して無駄にはならないのです。