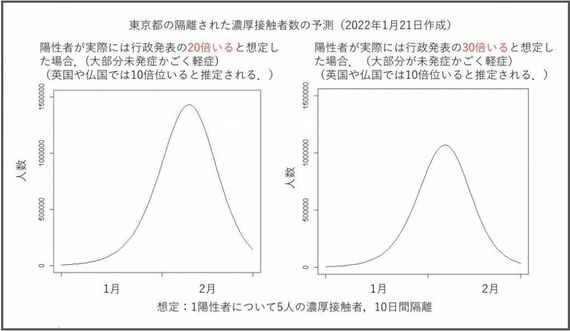
2月4日東京3万人超の予測もピークアウトは早い? 第2波“的中"土谷隆教授のシミュレーション
「悲観的かもしれませんが、そういうこともあり得ます。今やっている濃厚接触者の特定と追跡を続ければ、保健所の機能はパンクし、回らなくなるでしょう。行政が把握できない陽性者が街中にいて無意識に感染を広げている状態ですので、感染の実態を把握して拡大を防ぐうえでは、労力多くして効果が少ないやり方です」
感染者の広がりを把握するには、モニタリング検査で市中の陽性率を把握するほうがはるかに得策だという。
さらに、膨大な数の濃厚接触者が10日間(1月28日時点で)の自宅待機を余儀なくされれば、社会活動への影響も甚大だ。
「果敢に対策を変えていかなければなりません。重症化率の高いデルタ株とは違い、重症化が少なく感染拡大が早くて未発症感染者の多いオミクロン株でこれまでと同様の対策をとり続けるべきではないでしょう」
ただ、実際には、すでに保健所は濃厚接触者を特定する余裕がなくなっているため、「濃厚接触者が膨れ上がって社会崩壊が起こることはないというシナリオも考えられます」。
モデルは借金と利息の関係
土谷教授はどんなモデルに基づき、シミュレーションしているのか。感染症の広がりを表す数理モデルとしては京都大学の西浦博教授らが駆使する「SIRモデル」が有名だが、土谷教授がつくったのは、「SIRモデルを素朴に簡単化したもの」と言う。わかりやすく、借金の話にたとえて、説明してくれた。
「簡単に言えば、モデルの基本は感染者数の増加率を『金利』に見立てた、借金の総額を知る金利計算です。もちろん『変動金利』になっていて、感染対策をすれば金利は低くなるし、感染力の高い変異ウイルスが現れると、『金利』は高くなります。元本に金利をかけた数字が借金の額。それがその時点の感染者数です。ただ、それだけでは借金は増える一方なので、一定の期間がすぎると、一部を返済して元本が減る、つまり、治って感染者数が減るという仕組みを組み込んでいます」
微積分を使ったSIRモデルは難解だが、土谷教授の数理モデルは四則演算だけで構成されているので、ずっとイメージしやすい。
「新型コロナのような問題に立ち向かうためには、できるだけ多くの人に理解してもらえるようなモデルが必要と考えました。それによって導き出された予測がみなさんの生活に影響するわけですから」
多くの人が理解しやすいのはありがたいが、果たしてそれで「当たる」のだろうか。そんな疑念を吹き飛ばしたのは2020年7月。予測が世間を驚かせ、土谷教授の数理モデルが注目を浴びるようになった。
































