（第1回）円周率π～「円」に宿る深遠なる数～（前編）

●円を測る

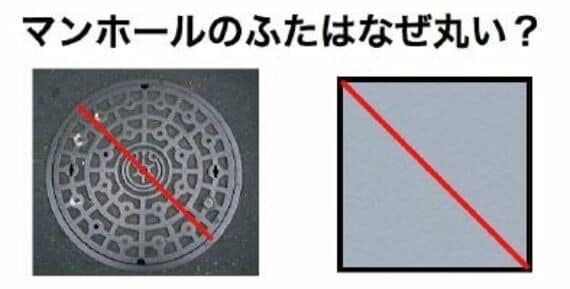
突然ですが、マンホールはなぜ丸いのか考えてみたことがありますか。何気ない風景にも理由があります。この絵をごらんいただきましょう。

もし四角だとすると、対角線の長さの方が一辺のそれより長いことがわかります。ですからちょっと蓋を回転させてしまうとこの鉄の重い塊は穴の中に落ちてしまいます。でも、蓋の形が円であればどのように回転させてもけっして落ちることはないのです。他にも円である理由があります。コロコロ転がし運搬がしやすい利点があります。これも、四角だったらそうはいきません。さらに、見た目にも円は気持ちがなごむ形ということがあるかもしれません。このように機能的にもデザイン的にも適した円は我々の生活の多くを支えているのです。僕たちの身体においても、目玉は丸いですし、関節運動はほとんど円運動です。それでも普段「円」を意識することはあまりないかもしれませんが、日本のお金は円、夫婦円満、円滑、…すべてに円は潜んでいるかのようです。
　その円の中に隠れている数が円周率πです。その定義は、円周の長さを直径で割った値です。すべての円、すなわちどんな直径の円であっても比は不変です。形を測るという作業を通じて数を発見する人間の営みが今から四千年前にはじまりました。今度は手を動かしてみてください。ここに、紙コップがあります。その口周りを測ってください。ただし使用していいものは定規、鉛筆、紙だけとします。さていかがでしょう。

2007年6月にパナソニックセンターのリスーピアという数学広場で私が行ったワークショップ「円描き大会」の様子です。今の問題はそこで提出したものです。さまざまなアイデアがでてくることに驚きました。

みなさんならどう測りますか。私の方法は、紙コップを逆さに紙の上に置き、定規に沿って滑らないよう一回転させるというものです。私のデータは、直径7.4 cm、口周り22.1 cmでした。次に電卓で22.1 ÷7.4 を計算してみます。結果は2.986 …約3.0 となりました。できるだけ精確に測ることで結果は3.14 に近づきますが、所詮mm精度の定規で紙コップを測ってみてもせいぜい3.1と小数点以下1桁までしかわかりません。小数点以下をさらに求めたいとするなら、定規の精度をあげるか、直径の大きなコップを測らなければならないでしょう。

●計算は旅　～イコールはレール～

僕にとって計算とは旅です。イコールはレールです。例えば、ピタゴラスの定理には＝があります。直角三角形の三辺の長さの間にa 2+b 2=c 2という関係が成り立ちます。すべての三角形に対してその等式が成り立つとピタゴラスは証明したのです。2500年前に証明されて以来今まですっとその真理は不動です。そしてこれから先、永遠にその真理は輝き続けていくのです。＝というレールの上を数式という列車が走る。そのレールは一度敷かれれば永遠に朽ちることがなく計算する者を運んでくれる。そんな風に計算や数式を考えることができると思うんです。