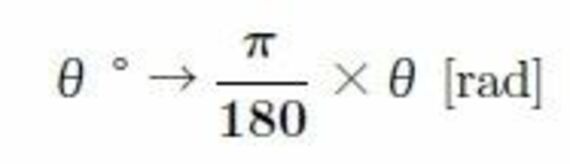（第1回）円周率π～「円」に宿る深遠なる数～（前編）

　それでは出発進行！古代エジプトですでに円周率が3.14と算出されています。アルキメデスは22 / 7 = 3.1428 …より小さいことを突き止めました。ちなみに、3月14日は数学の日、ホワイトデー、アインシュタインの誕生日（1879年）、数学者小倉金之助の誕生日（1885年）です。

有理数（分数）によるπの表示は小数点以下を多く求めようとすればするほど分数の分母・分子の桁数も大きくなってしまいます。ではどうやれば小数点以下を多く求めることができるのでしょうか。まさにこれが数学の歴史を貫く大きな課題といえます。本題にはいる前にπが現れる風景をみてみることにします。

●πとの出会い

三角関数sin、cosは円の中にその誕生の地があります。地球が丸いこと（球）、それに天体の軌道が円軌道と考えられたことからsin、cosが道具としてつくられました。球面三角法とはまさに球面上にある三角形（球面三角形）上を測る計算法です。東京とパリの緯度経度から距離が計算できます。地球が完全な球だと仮定した計算式で9730kmとでました。グーグルアースを使って東京とパリの距離を測ってみると9732kmなのでこの公式の精度はなかなかのものです。ここにはπが現れていませんが、角度θを度ではなく弧度法（単位[rad]）で測る際に、変換

をしなければなりません。ここにπが現れます。

ここで、eという数を紹介します。定数eはその値が2.718281828 …（鮒一鉢二鉢一鉢二鉢）という数理科学ではπと並んで重要な定数です。数学者オイラーEulerの頭文字がeの由来です。いったいどこに現れてくるのでしょうか。ヒントは肉まん、お茶、お風呂、そして富士山です。この4つに共通する数がeです。コンビニで売っている肉まんをケースから取り出した瞬間、手で持つには熱いです。しかし程なくして冷めてしまいます。お茶もそうです。お風呂にいたっては冷め具合はちょっと問題になります。よく家で母にお風呂が沸き上がるとはやくはいりなさいといわれたものです。はいらないでいると「お風呂が冷めちゃうでしょ、はやくはいりなさい」としかられたものです。冷め具合は最初が急激なのです。その後はゆっくりと冷めていくのです。これをグラフで表すと指数関数の形になる(t = 0 のとき肉まんと外気の温度差をT0とすれば、時間tにおける温度差Tは、T = T 0ekt (k は定数))のですが、その指数関数を表す数がeなのです。

eの別名はネイピア数、または自然対数の底ともいわれる所以がここにあります。富士山の美しさはその稜線にありますが、その形が指数関数によく似ていることに数年前気づき驚きました（正確には、x軸とy軸の比率をうまく変えてやると重なるように見えます。）。お風呂につかっていると温度は下がり続けます。それがeさんによる仕業なのです。富士山がいい眺めで、日本の風呂がいい湯なのはこのeのおかげなのかもしれません（笑）。