｢微分積分なんて実生活で使えないでしょ｣→使えるんです！郵送時に《レターパックプラスに詰め込める限界量》を｢微分｣で見極めてみる

式をゴリゴリ変形する前に、このV（x）が妥当かどうかを検討しましょう。x=0（つまり、高さゼロ）では、縦横はaとbでx=0なのでVは0。そこから少し大きくなると、Vは少しずつ大きくなっていきますが、2分のaに近くなってくると（a−2x）がゼロに近くなってくるので、Vは小さくなっていきます。つまり、この間に最大となる「ひと山」があるはずです。その山の頂上はどこでしょうか。

（画像：『マンガでわかる微分積分』）

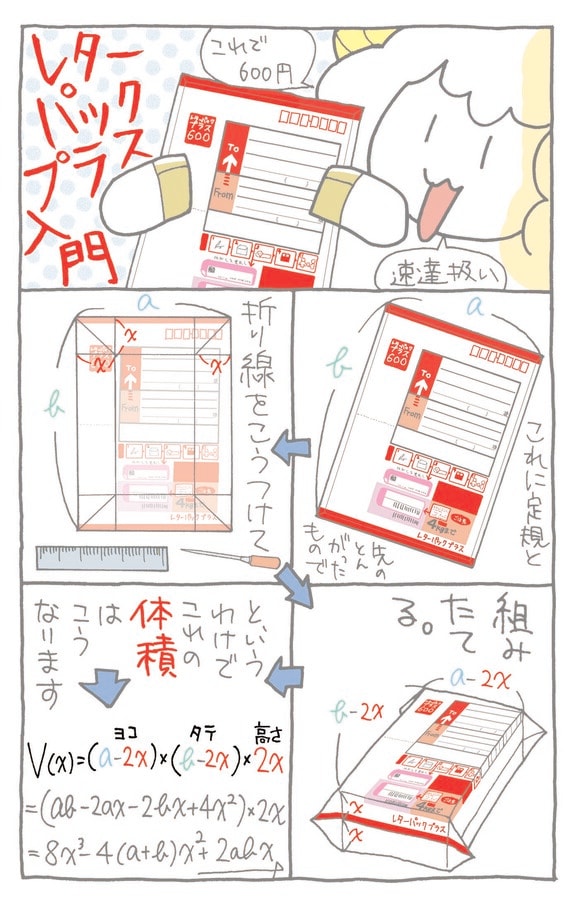
ほしい頂上の位置

頂上は、上りが下りに変わるところなので、傾きで言えばゼロになるところです。3次関数のグラフはたいてい2つの頂上があります（2つ目は頂上というより谷底ですが）。微分して=0とした2次方程式の解2つのうち、1つ目の解が、ほしい頂上の位置です。

（画像：『マンガでわかる微分積分』）

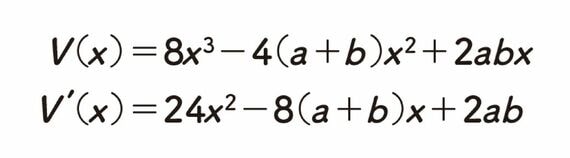
V′（x）=0になるxを探す、というのは、2次方程式を解けばいい※1ので、解いてみると、

（画像：『マンガでわかる微分積分』）

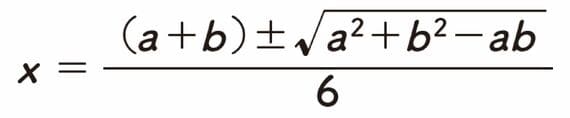
このうち1つ目の解というのは、小さいほうのことなので、±のうち−のほうになります。

したがって、頂上の位置は、

（画像：『マンガでわかる微分積分』）

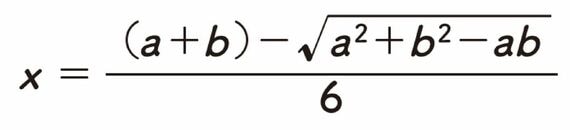
ということになります。これにa=248mm、b=340mmを代入して計算すると、x=47.2mmが得られるので、そのときの体積は3561cm3≒3.5リットルとなるのです。