東京理科大｢数学で出題ミス｣広がる学生の動揺 どこが出題ミスだったのか？徹底解説する

大半の受験生は「部分分数分解をうまく使えるはずだよな？でも、うまく計算できない。何か計算ミスをしたんじゃないか」と、戸惑ってしまい、答えを出すことはできなかったのではないかと考えられます。実際、東大生の友達数人と解いてみたのですが、「解けそうで解けない式になってしまい、何かがおかしい」という感想でした。

全員正解＝受験生全員に平等か？

この出題ミスに関して、東京理科大学の公的な措置は「出題ミスを全面的に認めたうえで、(4) に関しては、全員正解と取り扱う」というものでした。しかし、ほかに対応方法がないとはいえ、この対応で受験生たちが平等になるということではないと思います。

「(4) が解けないということは、(2) までの時点で、何かミスをしているのではないか？」と思ってしまった受験生は、本来必要のない見直しのために試験時間を浪費してしまった可能性があるということです。出題ミスがあった場合に「該当の問題に関して全員正解」と扱う対応は、確かに一般的な対応ではありますが、今回に関しては、

・数学の、しかも記述式の試験であったこと。

・(4) の設問がミスリーディングであり、他の小問の解答にも影響を及ぼし得ること。

これらを考慮し、画一的な対応ではなく、各受験生の解答状況を鑑みて個別の対応をしてほしかったとも思います。

さて、さらに出題ミスの部分をより詳しく数学的に解説します。なお、以下に述べる改変案は、筆者個人の見解であり、2025年2月26日現在で、公式の発表がなされているわけではないことに留意ください。

これに関して、おそらく出題者は、

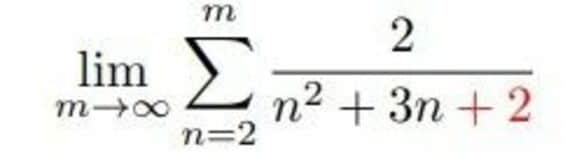
という値を計算させるつもりで、この問題を出題しています。 これを正当化しようとすると、本来の問題文は次のようなものだったのではないかと考えられます。

これを先ほどと同じように図示してみると、以下のようになります。

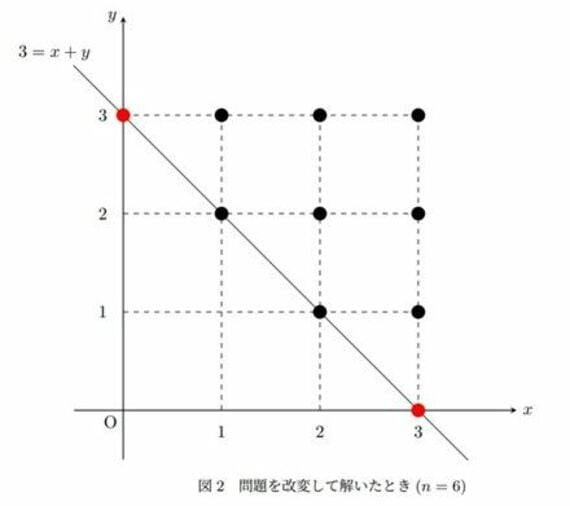
つまり、端っこ2つの点を数えるか、数えないかという違いということです。 原文（出題ミス）のときには端の点を数えず、改変案のときには端の点を数えています。

ただ、点を数えるときに、端の点2つだけをあえて数えないという操作は、少し数学的に不自然な操作です。