数に強い人なら｢5秒で解く｣分数だらけのクイズ 1から｢10個の分数を引き算｣を一瞬で解く工夫

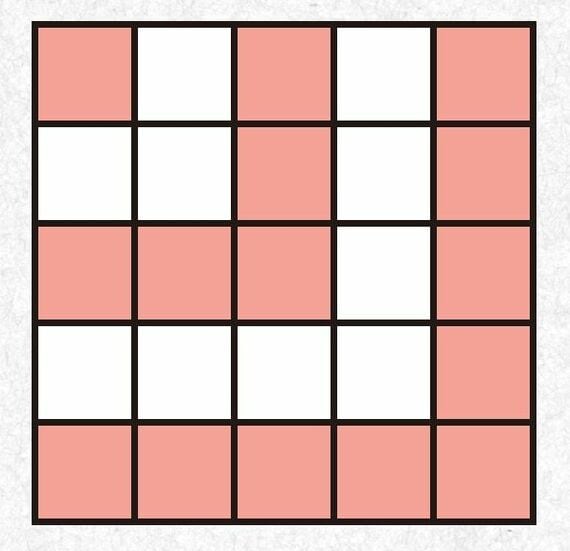
1タイルが1cm×1cmの正方形を敷き詰めて、新しい正方形を作っていくことを想像してください。1タイルの正方形を作った後、2cm×2cmの正方形を作るためには、右下に逆L字のタイルが3つ必要ですね。これで、1つのタイルに3つのタイルが加わって、4タイルの正方形ができました。

では、次に3cm×3cmの正方形を作るためにはどうなるでしょう？ これも、同じことですね。4タイルに加えて、右下に逆L字のタイルが5つ必要です。これで4＋5＝9タイルの正方形ができます。

もう気づいた人もいるかもしれないのですが、この「正方形作り」と「1＋3＋5＋7＋……」の計算は、一緒です。この正方形の面積が、奇数の足し算の合計と同じ数になるのです。

だから、3番目までの奇数の合計は3×3の正方形の面積と同じで9に、4番目までの奇数の合計は4×4の正方形の面積と同じで16に、50番目までの奇数の合計は50×50で2500になるのです。

このように、図に直す思考はとても有効です。計算式を正方形に置き換えてみたり、碁石を使って考えてみたり、タイルを置くように考えてみたり……。

「直感的にわかりやすい」はやるべきことの整理にも

他にも、東大生は自分のやるべきことの優先順位を考えるために、マトリクスで考えるという思考法を実践している人も多いです。例えば、X軸を「すぐにおわるか時間がかかるか」、Y軸を「締め切りが早いか先か」で分けてグラフを作ると、このようになります。

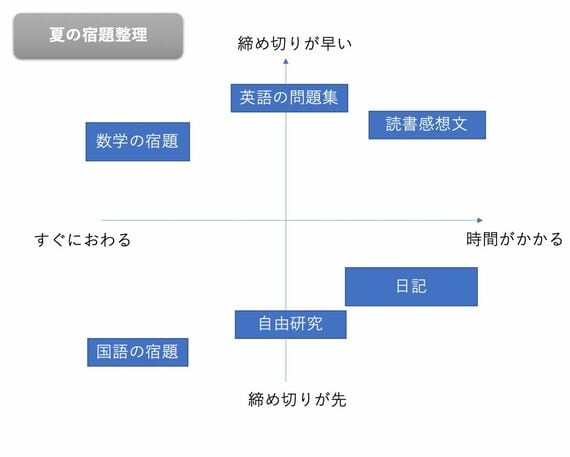
こうすれば、やるべきことが可視化されて、どれから手を付けるべきなのかが明確になっていきますよね。

数式ややるべきことを図式化する思考法は、いろんな場所で応用できるものです。算数や数学の問題を解くだけでなく、実社会でも応用可能なものなのです。

この思考法をぜひ、意識してみてもらえればと思います。