東大生解説､数学嫌いでも｢積分｣学んでほしい根拠 理屈は難しくない！考え方を知ることで広がる視点

面積を求めることで、時間によって速度が変化する物体の移動した距離の合計が求められてしまう、という事実は困惑する人も少なくないかもしれません。その場合は、速度が一定だったとして考えてみましょう。

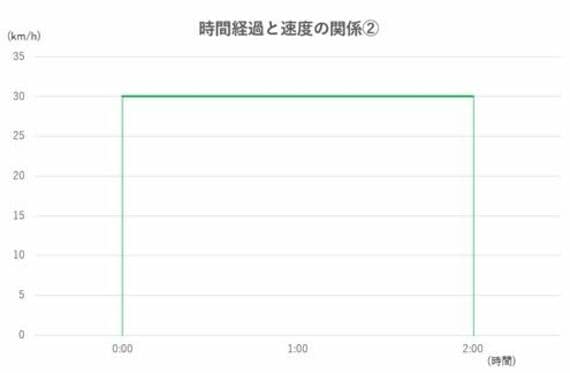
このように、例えば一定の速度「時速30km」で車を2時間走らせた場合、車が進んだ距離は「時速30km×2時間」で60kmとなります。これは、縦の長さ30、横の長さ2の長方形の面積の値と同じになります。速度が一定でなくても、同じように面積を考えれば移動した総距離は求められるのです。

球体の体積を求める方法も積分で出せる

この積分の足し合わせる概念は、世の中のさまざまな場所に用いられています。

例えば皆さん、バレーボールのような球体の「体積」の求め方を覚えていますか。小中学校の数学で習うこの体積の求め方は、体積を「V」とすると

「V＝4/3 πr³ （πは円周率3.14… rは球の半径）」

と表されます。この公式を学生時代に頑張って覚えたという人も多いと思いますが、この公式にはもちろん積分によって編み出されています。球体を薄い円がいくつも連なってできたものだと捉え、その1つひとつの円の面積を足し合わせて全体の体積を出しているのです。

実際に数式で見てみましょう。積分の公式を解説すると難しくなるため、ここでは例示しませんが、ここでは「r」を積分すると「1/2r²」になり、「r²」を積分すると「1/3r³」となるということだけ覚えておいてください。

円の面積を「S」とすると、「S＝4πr²」と表されます。Sをrで積分すると、r²→1/3r³となることから、4πr²→4/3πr³（＝V）となります。

微分積分の考え方は、概念を理解していれば数学以外の場面でも応用することができます。物事を分解して、その一瞬一瞬での変化を捉え、それを合わせることで全体の動きを測る。この考え方を知っていると物事を分析する際の視野が広がると思います。