東大生解説､数学嫌いでも｢積分｣学んでほしい根拠 理屈は難しくない！考え方を知ることで広がる視点

積分とは、数学や物理学などの領域で用いられる概念です。時間によって変化する事柄や、片方の値に応じてとる値が変化する関数を、範囲を定めて数値的に評価することができます。この積分を使うと、先ほどの問題はこのように考えることができます。

以下のグラフでは、横軸を時間、縦軸を速度としています。また、車を走らせ始めた時間を「0」として、それぞれの時間ごとの速度変化を表しています。

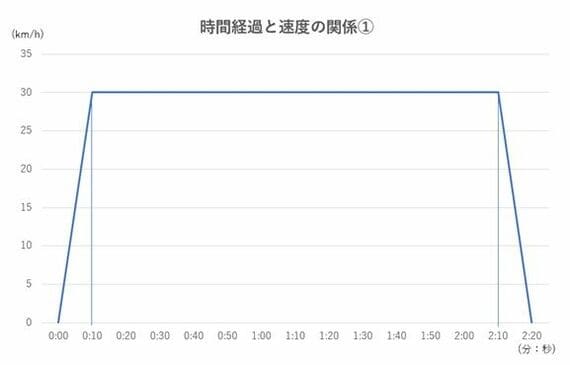
問題条件に合わせて速度を考えると、最初の10秒間は右肩上がりのグラフ、時速が一定になってからの2分間は横軸と平行な直線に、ブレーキを踏んで停車しようとしている最後の10秒間は右肩下がりになります。

実は積分の考えを用いると、このグラフと横軸（時間の軸）でできる図形の面積を求めることで問題の答えである「進んだ距離」がわかるのです。

台形の面積を求める公式で計算してみる

この問題の場合は、台形の面積を求める公式を用いてみましょう。台形の面積は、

「（上底＋下底）×高さ÷2」

で求めることができます。今回の場合において、上底は「2分」、下底は「2分20秒」、高さは「時速30km」であるため、求める答えは

（2分＋2分20秒）×時速30km÷2＝時速30km×2分10秒＝1km+1/12km

つまり、加速と減速の部分で1/12km、80m以上も進んでいることになるのです。