｢プレミアム付商品券｣に飛びつく人に欠けた視点 数学的視点で本当に｢お得｣なのか見極める

カレーの「辛さ」を「ヴェーバー＝フェヒナーの法則」にあてはめると、「感覚の強さ（辛さ）＝（定数）×log（刺激の強さ⇒香辛料の量）」となります。カレーの辛さが1（＝現状の辛さ）のときの香辛料の量を10としたとき、法則を利用して計算すると、その結果は下記の図の通りです。

（出所）『世界が面白くなる!身の回りの数学』より

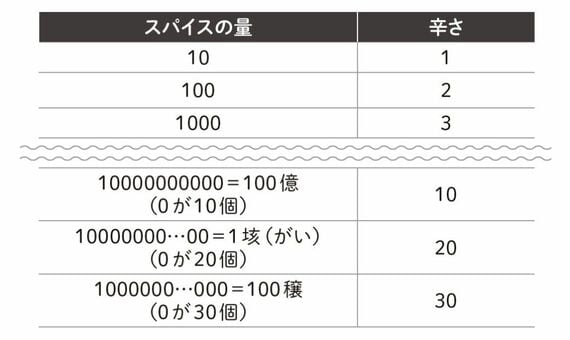
スパイスの量とカレーの辛さの変化

この図からわかるように、香辛料を3倍の量に増やしても辛さはさほど変わりません。3倍の辛さにするには、なんと1000の量の香辛料が必要となるのです。

法則に出てくる「log（対数）」とは大まかにいうと、掛け算した回数を表す記号です。今回は、辛さ1のときに香辛料を10としているため、香辛料の量100や1000の辛さはそれぞれ、下記のように式を変形しlogの計算をします。

100＝10×10  
 1000＝10×10×10

1000は10を3回掛け算しているので、logの計算結果は3で辛さは3となります。このように、掛け算した回数を表す記号がlogです。なお、この場合は掛け算した回数＝logは0の個数を数えることで求めることもできます。

100⇒0が2個  1000⇒0が3個

そして、「ヴェーバー＝フェヒナーの法則」にあてはめて、香辛料10のカレーを3倍の辛さにするには、10（定数）×100となり、香辛料は1000を必要とします。現状の辛さのときの香辛料の100倍の量が必要になるというわけです。

『世界が面白くなる!身の回りの数学』（あさ出版）。書影をクリックするとAmazonのサイトにジャンプします

このように、「数学」は私たちの身近に存在しています。「60%割引」と「60%ポイント還元」を同じように捉えている人や、カレーの辛さを3倍にするには香辛料も3倍にすればよいと考えている人がいるかもしれません。直感はときとして事実とはまったく違った認識を生むことがあるのです。

日常のさまざまな課題は数学的思考を用いることで正解、または良き解にたどり着いたり、そこから“意外な事実”を発見したりできます。ビジネスシーンでも、数学的思考を使って課題に取り組むことで、より良き解にたどり着けることは少なくありません。