筆算の仕組み｢説明できる人｣｢できない人｣の差 頭がよくなるためにやりたい思考の癖づけ
2桁以上の数字の掛け算をするときにも当然のように使用する、筆算。小学校で習う方法ですが、こちらも「なぜ筆算で計算ができるのか」と考えたことはあるでしょうか。この簡略化された方法も、実のところ、
a × ( b + c ) = a × b + a × c
という分配法則を用いてそれを縦に圧縮して書いているだけなのです。1つひとつの操作をひもといていくと、実に合理的にできていることがわかります。
筆算を使わずに2桁の掛け算、できる？
ではここで問題です。
47×36はいくらになるでしょうか。
筆算の計算を書いてしまえばあっという間ですが、今回は違う方法でアプローチしていきます。問題の式ですが、一般的に2桁の数は、
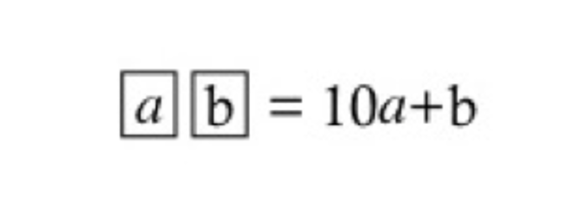
で表すことができます。23であれば 20×2＋3で表せるということです。続いて、
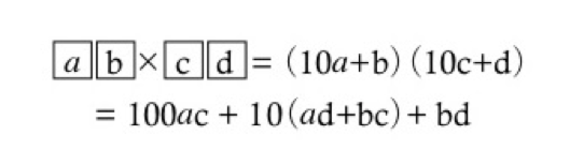
と表すことができます。つまり、
このようになるのです。ここまで分解したものを踏まえて、下図をご覧ください。
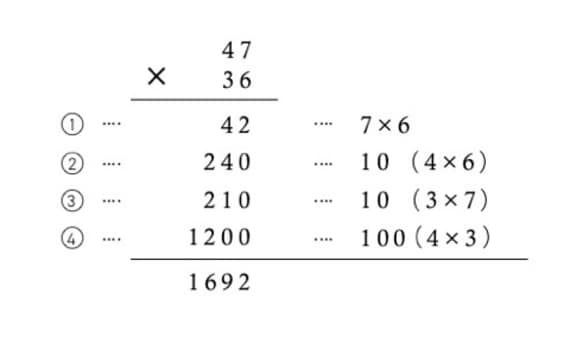
この図の①と②、③と④を合体させたものが、
トピックボードAD
有料会員限定記事
キャリア・教育の人気記事
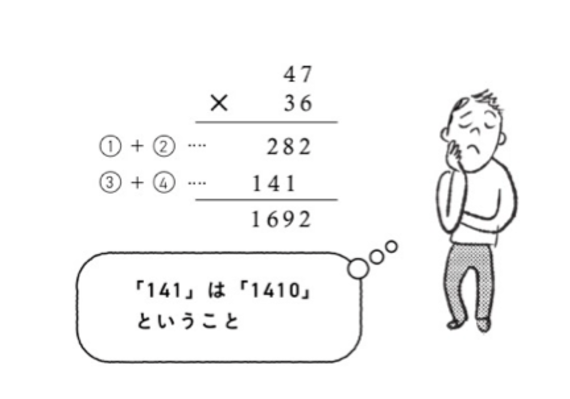
無料会員登録はこちら
ログインはこちら