筆算の仕組み｢説明できる人｣｢できない人｣の差 頭がよくなるためにやりたい思考の癖づけ

では数学でどんな思考が鍛えられるか。それは圧倒的に論理的な思考力だと私は思います。なぜなら数学ではいろんな条件を使いながら、筋道を立てて、問題を解いていきます。不必要な条件や、問題に適さない公式や定理などは除外し、適切な方法を考えながら、正しい答えへとたどり着くのです。

数学を学ぶということはそのまま論理的な考え方を鍛えていると言っても過言ではないわけです。

割り算の筆算、大きい位から行うのはなぜ？

ではここで問題です。

52342÷3 はいくらになるでしょうか。

割り算の筆算は大きい位から行いますが、それはなぜでしょうか。ただの数字で計算してもイメージがしにくいので、52342円を3人で分ける場合を考えてみましょう。

金額を 1円玉に両替して、トランプを配るようにそれらを 分ければ確実ですが、普通はそうはしませんね。なので、まずは5枚の1万円札を3人で分けます。すると 1人1枚で 2枚の1万円札が余ります(この時点で1人あたり 1万円)。

もう 1万円札で分けることはできませんので、次は1000円札で分けようとなります。あまった2万円を1000円札 20枚に両替して、もともとあった 2枚と合わせて 22枚の1000円札を 3人で分けます。すると、22を3で割って 7余り 1。 つまり、1人7枚(= 7000円)で1000円札1枚が余ります。

お金は公平に配らなければならないので、万から千、千から百としたように、100円から10円、10円から1円と、各位の余ったお金を下の位に両替して、割っていきます。その操作が下の図になります。

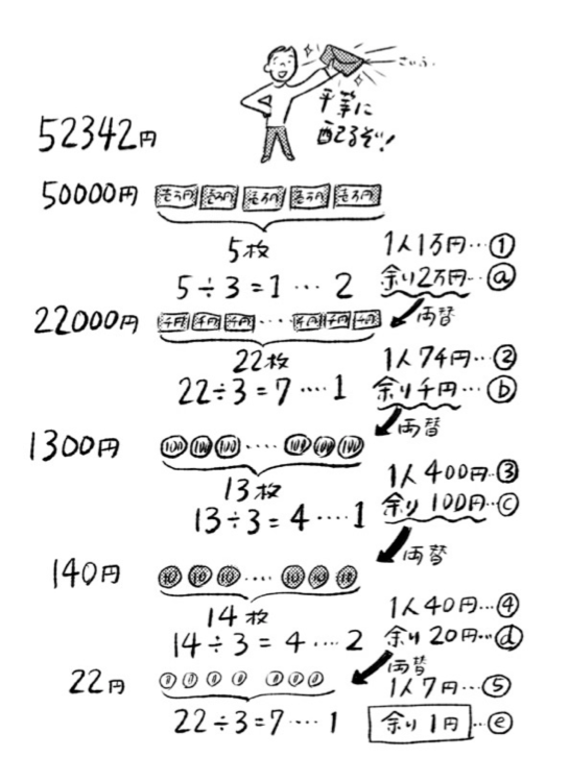
そうすると最後の 1の位までいくと 1円が余ります。1人に配るお金は上記の①から⑤までの総和で求めることができ、1人17447円を配ったうえで、1円余るということです。

筆算とは、このような操作をスピーディかつミスをしないために、実に合理的なやり方になっているのです。小学校では「こうなるから、これを覚えて計算しましょう」と計算ドリルをひたすらやらされたことでしょう。しかし、実際に割り算の操作がどのような仕組みになっているのかということを考えてみると、無駄をそぎ落とした計算方法だということがわかるのです。