牛乳パックの｢なぜ｣で伸ばせる子どもの創造力 ｢考える子｣を育てるために大事な3ステップ

「知恵」という言葉は、だれもが知っているだろう。仏教で「智慧」という場合、それは「聞慧（もんえ）」「思慧（しえ）」「修慧（しゅえ）」の3つの「三慧（さんえ）」から成り立つという。

聞慧とは、授業で聞いたり本を読んだりして、聞いたことや書いてあることを事実として知ることである。

思慧とは、聞慧として身につけたものごとに関して、自分なりにそれらの間のつながりを組み立てたり、それらの背景を理解したりすることである。

最後の修慧は、思慧として身につけたものごとに関して、きちんと説明できるように書いたり、それらを応用して実践したりすることができるようになる段階である。

具体的に中学数学で学ぶ「三平方の定理」によって、三慧を説明してみよう。

三平方の定理とは、角C＝90度、BC＝a、AC＝b、AB＝cである直角三角形ABCにおいて、次の式が成り立つことをいう。

aの2乗＋bの2乗＝cの2乗

これは「直角をはさむ2辺の長さをそれぞれ2乗したものの和は、斜辺の長さの2乗に等しい」ということを示している。その事実は知っているものの、その証明を理解したり、その応用問題を解いたりしたことがない状態は、まだ聞慧の段階にとどまっている。

次に、三平方の定理の証明を自分なりにしっかり読んで理解し、2辺の長さが具体的に与えられている直角三角形のもう1つの辺の長さを求められるようになる状態は、思慧の段階に達したといえる。

さらに、三平方の定理の証明を他人にわかるように説明でき、例えば富士山頂からの視界のような応用例を他人に面白く話せるようになると、それは修慧の段階に達したといえる。

東京に富士見町がある「ふしぎ」

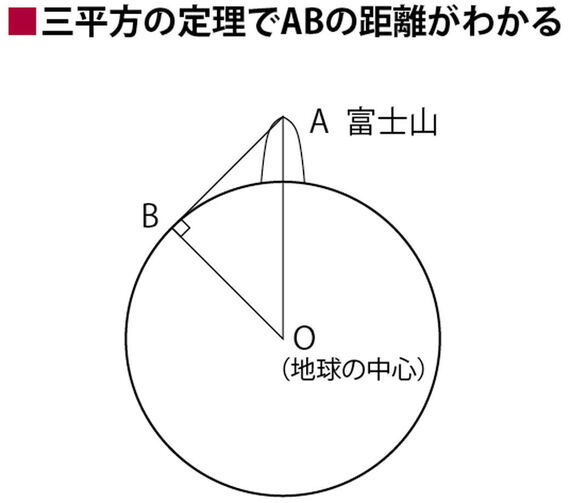
例えば、こんな説明ができたらとてもよい。富士山の頂上（A）と地球の中心（O）、富士山頂から見渡せる地球上（海抜0m）の最も遠いB地点という3点があるとして、その3点を結ぶ直角三角形ABOを考えてみよう（ABとBOに挟まれた角Bが直角、図参照）。

出所：芳沢光雄『AI時代に生きる数学力の鍛え方』