アリにとって最も重要なのは、問題を具体化する方法、つまりHowである。対するキリギリスに必要なのは目的、つまりWhyである。変数を最適化するために必要な問いがHowで、変数そのものを探すために必要な問いがWhyだからである。
具体化という言葉が出てきたところで、抽象と具体というのも同様の関係である。具体の世界だけ見ていても、問題の発見は表面的なところにとどまって、本質的なところまでは見えない。抽象化によって、その問題が内包する本質的な課題が浮かび上がり、それによって「壁を超えて」考えることができるのである。
具体と比較した抽象とは、よくも悪くも「自由度が高い」状態である。具体的であるものは「すぐに実行が可能である」という点で、問題解決型のアリには最も重要なものであるが、キリギリスには「応用が効かない表面的な事象」と写るのである。
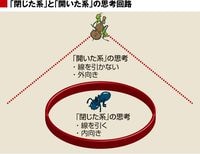
アリとキリギリスの思考の違い
「変数が固定されている」アリは、問題解決がうまくいかなかったときにそれを他者や環境の責任にする、つまり「他責」かつ被害者意識になりやすい。
なぜなら、固定された変数の中で与えられた問題を解決することのプロフェッショナルであるアリは、その問題を解くことには全力を尽くす代わりに、それがうまく行かなかった場合には、「与えられた問題（変数の定義）そのものが悪い」と考えるからである。変数そのものを増減させて「問題そのものを変える」という選択肢がもともとないアリにとっては、自分は全力を尽くしているのだから、あとは悪いのは「問題を作ったほうだ」という姿勢になるのである。
対してキリギリスは、問題そのものが悪ければその問題そのものを解くのをやめて、自分で別の問題を定義し始めるのである。そうした高い思考の自由度を持っているキリギリスは、すべての問題が自分の考え方次第で何とかなると思っている。だからつねに矛先が自らの創意工夫に向くのである。
またアリはむやみに「自由度を増やされる」ことを嫌う。変数が増えれば、それだけ問題が複雑になって解決するのも大変になるからである。ここでキリギリスとの対立が起こる。
「跳び道具」を使って変数を増やし、思考の自由度を上げることで「広い世界」を見ているキリギリスは、もっと「高く」飛び立てば、すばらしい世界が広がっていることを知っている。だから、変数を固定して「狭い平面の世界に閉じこもっている」アリが歯がゆくてたまらない。
ところがこれは、壁の外に出たくても出られないアリにとっては、「大きなお世話」以外の何ものでもないのである。どうせ外に出られないのであれば、変数を固定して（たとえそれが「つまらない」問題であろうが）さっさと解決したほうがましなのに、「外の世界のすばらしさ」を語るキリギリスが疎ましくて仕方がない。
これは経営者と一般従業員、あるいは「意識の高い」上司と「意識の低い」部下との間で頻繁に起きる構図である。ここでいう「変数」とは、たとえば各人が持っている権限の範囲を意味する。「アリとキリギリス」のお互いの思考回路やスタンス、あるいは制約条件を理解すれば、相手の気持ちが理解できるだろう。
次回はさらにこうしたアリとキリギリスの対立構造のメカニズムを紹介するとともに、イノベーションを活性化するための両者の最適な活用方法について解説する。
ログインはこちら