キリギリスは思考の自由度が高い 「固定次元」のアリから「可変次元」のキリギリスへ

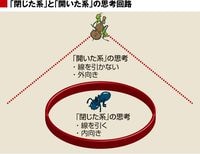
つまり、次元をひとつ追加することで行動の自由度が増し、2次元ではできなかったことが可能になる。前回述べた「閉じた系」のアリが「開いた系」のキリギリスになるためには、「次元を上げる」ことが必要ということだ。

アインシュタインは「われわれの直面する重要な問題はその問題を作ったときと同じレベルの考えで解決することはできない」という言葉を残しているが、まさにこのイメージである。

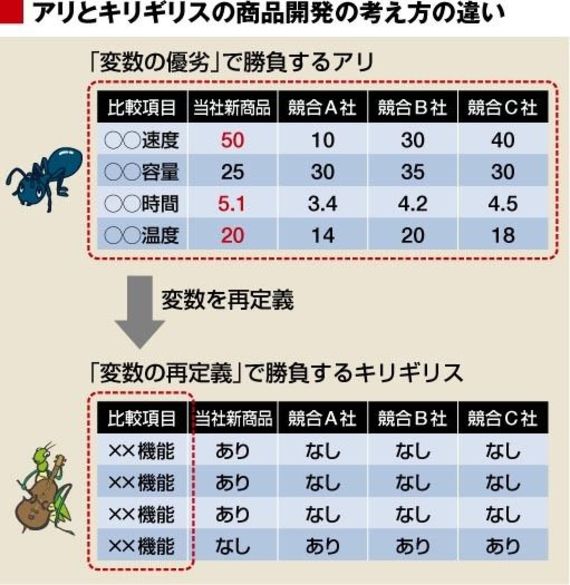
商品開発におけるアリとキリギリスの考え方の違い

先述のとおり、「次元」とは、「思考の自由度」のことであり、考えるための「変数」のこととも言える。「変数（の種類）を固定して考える」アリと「変数を増減させて考える」キリギリスとの考え方の違いを、新しい商品やサービスを考える場面で比較してみよう。

ここでの「変数」は、製品のさまざまな仕様や性能（の種類）と考えてよい。たとえば、自動車で言えば、エンジンの排気量、車体重量、外形寸法、燃費……といったところだろうか。

変数を固定して考えるアリは、これらの性能の数値において他社を上回るものを開発しようとする。したがって、まず（頭の中で）することは、現状ある変数を列挙し、それを競合他社と「比較」して、数値でそれを上回ることである。