キリギリスは思考の自由度が高い 「固定次元」のアリから「可変次元」のキリギリスへ

イメージをつかむために、次のマッチ棒パズルの問題を考えてみてほしい。

【マッチ棒6本を使って正三角形を4つ作るにはどうすればよいか？】

この問題はマッチ棒パズルの「常識」とも言える、「平面」の2次元の世界だけで考えていては簡単には解けないが、「高さ」を持たせて3次元空間で考えるという選択肢を思いつけば、すぐに解答にたどり着けるはずである（解答例：「正三角錐」を作る）。

さらに、2次元を3次元に上げることによって「解けない問題を解く」別の例を、「アリとキリギリス」の比較によって行ってみよう。

アリが1匹、「壁」のようなもので囲まれている状況を想定する（下図）。

壁の高さはアリの体高よりは何倍か高いために、アリには単なる（上限の見えない）「塀」に見えている。その外側にアリの好物が置かれており、そのにおいから、アリは「塀の外側」に何か魅力的なものがあることだけはわかっている。

さて、このアリは餌にありつくことができるだろうか？

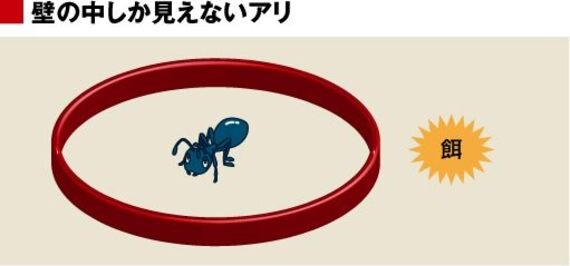
少なくとも何らかの「飛び道具」を使わないかぎり、アリはその塀の外側に出ることはできないだろう。アリの行動範囲は基本的に平面上の移動という「2次元」の世界だけだからである。

ではこれがキリギリスだったらどうだろう？ 「ジャンプする」という、文字っどおりの「跳び道具」を持っているキリギリスにとって、塀は簡単に超えられる。

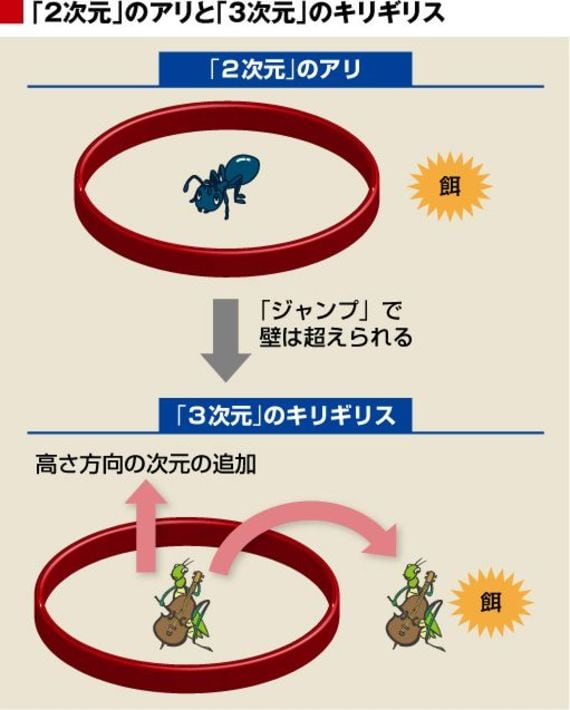
これはキリギリスが「高さ」というもうひとつの次元を移動することができるからである。