東大生伝授､使えると便利｢片手で31まで｣数える術 知ると視野が広がる｢n進法｣の興味深い世界

話を戻しましょう。ここまで説明した2進法の考え方を応用すると、片手でより多くの数を表すことができるのです。

親指から小指までの5本の指において、それぞれ指を「開いている」状態と、「折っている」状態の2種類が存在します。

この2種類にそれぞれ「開いている」場合は「0」、「折っている」場合は「1」というふうに2進法の数を対応させます。そして「親指だけを折っている状態」を「1」、「人差し指だけを折っている状態」を「10」というふうに2進数で表してみましょう。

すると、それぞれの指に対して2種類の状態があるため、片手の5本の指の状態は2の「5乗」で32通り存在することがわかります。よって、「1から32まで」、あるいは「0」を含めて「0から31まで」の数字を数えることが可能になるのです。

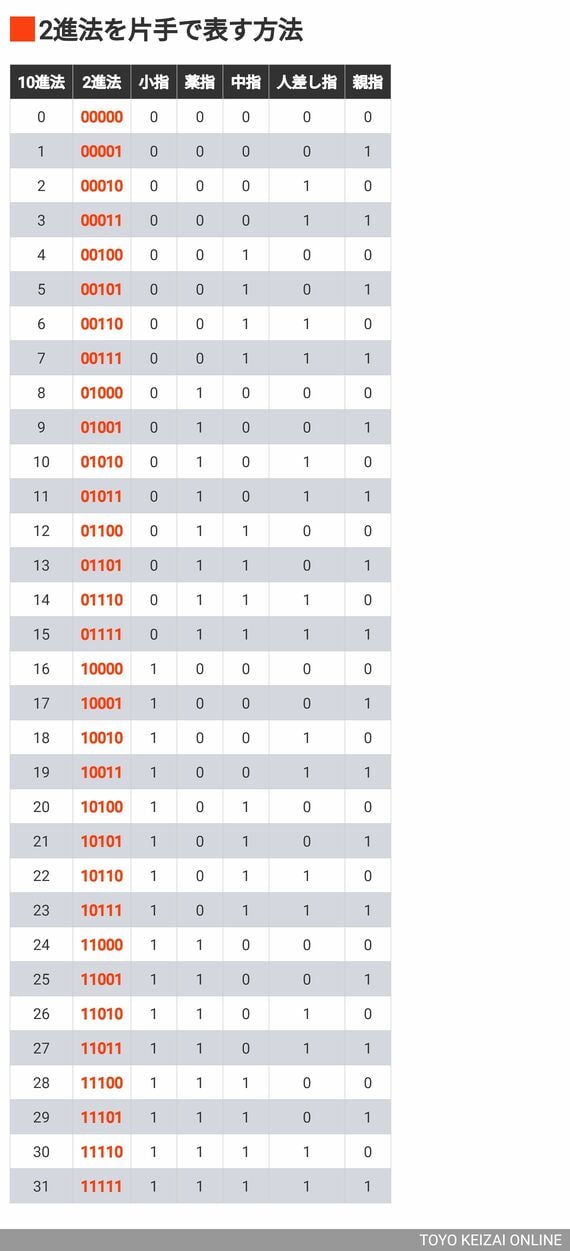
※外部配信先では図を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください

いかがでしょうか。5本しかない指を用いても、指の状態を2進法に生かすことによってより多くの数を数えられるようになります。数学の数の考え方は、このような意外な場面で生かされているのです。

普段使っている「10進法」の弱点

さて、この「2進法」や「10進法」という数の記法はまとめて「n進法」と呼ばれています。このn進法に関しては数学用語だと思っている人も多いと思いますが、実は日常のあらゆる場所で用いられているのです。

まず、われわれが一番自然に使っている数の表し方が、先ほども説明した通り「10進法」になります。10をひとまとまりとする考え方で、一説によるとこれが一番強く根付いたのは両手の指の数が合わせて10本であるから、ともいわれています。

しかしこの「10進法」には弱点があります。それは、「分割しにくい」ということです。

10個のお菓子をグループのメンバーで分けるシチュエーションを考えてみてください。人数が3人でも、4人でも割り切ることができません。10という数字は1とその数字以外の約数が2と5しかないため、分割にあまり適していないのです。