｢食べ放題だとすぐに満腹｣はなぜか､数字で検証 東大クイズ王が伝授｢論理的に考える思考法｣

下の図のように、まず「AならばBである」という「命題」があるとします。このとき、「BならばAである」は元の命題の「逆」、「AでないならばBではない」は元の命題の「裏」、そして、「BでないならばAではない」は元の命題の「対偶」といいます。

『文系でも思わずハマる 数学沼』より

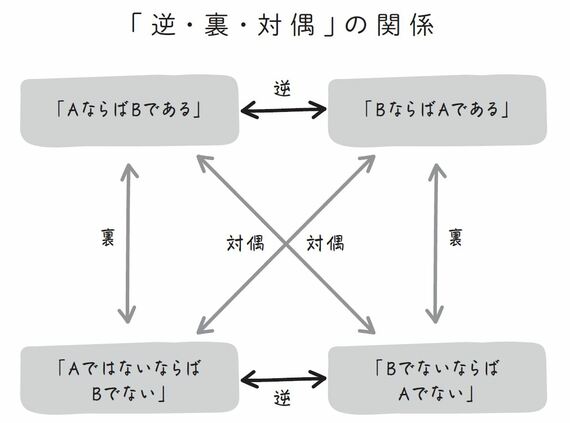
ここで、ある命題とその対偶との間には、「命題が真である（正しい）とき、その対偶もまた真である（正しい）」という関係が成り立ちます。これを利用することで、正しい結論を導き出そうというのが、対偶法です。

さらに、よりわかりやすい例を挙げると、「人間は皆、死ぬ」という真の命題があります。このとき、「人間である」ことをA、「死ぬ」ことをBとすると、この命題の「逆」は、「死ぬならば、人間である」となります。また、この命題の「裏」は「人間でないならば、死なない」となります。

しかし、逆も裏もどちらも真ではないですよね。

一方、対偶は「死なないならば、人間ではない」となります。これは確かに真です。このように、命題が真であるとき、その対偶もまた真である一方で、逆と裏が真であるとは限りません。

答えの導き方を検証してみる

では、最初の問題に戻って、検証していきましょう。

ここで、「アルコール飲料を飲んでいるならば」をA、「20歳以上である」をBとします。「AならばB」の対偶は、「BでないならばAではない」ですので、まず、命題が真であることを確かめるため、「ビールを飲んでいる人が20歳以上である」ことを確かめます。

次に、対偶が真であることを確かめるため、「17歳の人がアルコール飲料を飲んでいない」ことを確かめます。それにより、ルールが守られていることを確認できるというわけです。

一方で、28歳の人を確認することは、命題の「逆」を確認することであり、「20歳以上ならば、アルコール飲料を飲んでいる」ということになります。