｢謎解き｣が苦手な人が知らない2つの重要視点 頭が凝り固まっていないかをチェック！

すると、

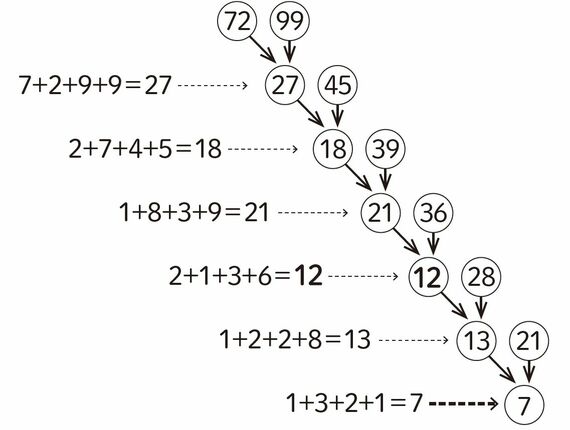
1＋3＋2＋1＝7

となり、見事に関係が成り立つことがわかります。この法則を問題のパズルにあてはめて、上から再度計算してみます。新しく発見した法則に従って計算すると、他のパズル部分の数字とぴたりとあてはまります。この結果、「？」部分は12と答えを導き出せるのです。

数学は失敗の先に正解がある学問

この問題から私がお伝えしたかったことは2つあります。

ひとつは、うまくいかなかった方法を経験し、失敗から改善方法を考えることの重要性です。これは数学力を向上させる大事な要素のひとつです。勝負の世界では「勝ちに不思議な勝ちあれど、負けに不思議な負けはない」と言われます。この格言は数学にも通じます。

『世界が面白くなる!身の回りの数学』（あさ出版）。書影をクリックするとAmazonのサイトにジャンプします

問題を解く際には正解に至るプロセスはひとつとは限りません。そのため、ロジカルな考え方に基づいた解答ではなく偶然に正解することもあります。しかし、それはたとえ正解したとしても偶然による結果です。

一方で、失敗は偶然ではないので、理由を考えることができます。ある問題をAという方法で間違えたら、次の問題ではAの方法は控えようと判断できるようになります。失敗の経験の先に正解への道筋が開かれているのです。

もうひとつは、数学で使われる法則はどんな状況でもその法則が成り立たなければ認められないということです。この問題では最初は引き算する方法を使いましたが、最後のパズル部分では法則が成り立ちませんでした。

たとえ100番目まではうまくいったとしても、101番目にうまくいかなければダメ。それが数学なのです。