ビジネスマンに必要な｢数学センス｣の磨き方 テスト勉強では身につかない､数学の面白さ

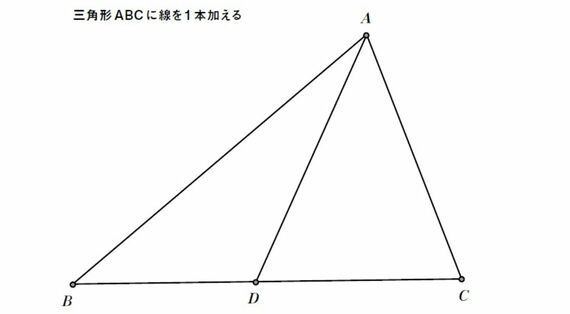
上の図には、三角形が3つしかない。つまり△ABC、△ABD、△ACDだ。ここでもう1本の直線BFを加え、三角形の数を数えてみよう。

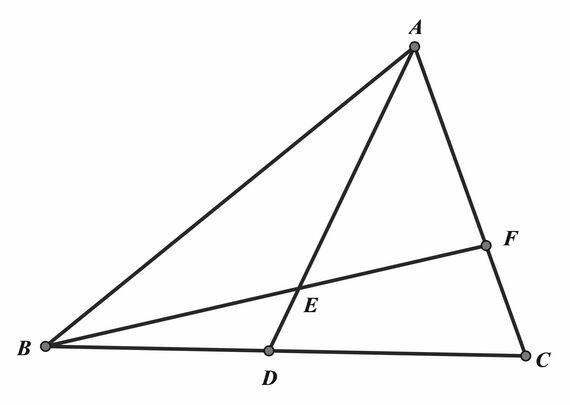
線分BFを引くと、次に挙げる三角形はその線分、あるいはその一部を辺として使っていることがわかる。△BED、△ABE、△ABF、△AEF、△BFCだ。

次に3本目の線分を加え、もともと示してあった図を完成させ、辺として線分CKを、あるいは辺として線分CKの一部を使っている三角形をリストアップする。以下のような三角形だ。△BGC、△BKC、△HEG、△DHC、△BKG、△AKH、△AHC、△GFC、△AKCだ。

ばらばらにする方式でアプローチ

こうして、元の図には合計で17の三角形が見られる。それらを比較的簡単に数えあげられたのは、1つずつ図形を再構成し、線分を加えると見えてくる新たな三角形をその都度数えたからだ。一般的にこれは、問題が一見して解けそうもないと思える場合に役に立つ手段だ。

この種の問題、つまり、ばらばらにする方式でアプローチすると極めて簡単に解決できる問題には、次のようなものもある。