錯覚から探る「見る」ことの危うさ《第3回》--不可能ではない「不可能立体」

2011/12/22 0:01

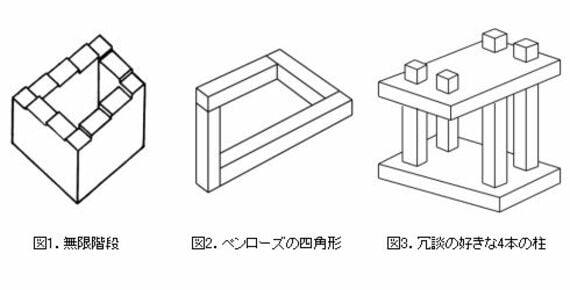
不可能立体の絵と呼ばれるだまし絵がある。図1、図2、図3がその代表的な例である。
　
　図1は、中庭のある建物の屋上に作られた階段で、登り続けると出発点に戻るというありえないことが起こってしまう。「無限階段」と呼ばれている。このだまし絵はオランダの版画家エッシャーが作品「上昇と下降」（1960）の中で使ったことでも有名である。
　
　図2は、ペンローズの四角形と呼ばれており、ひねりが加わった形で角材が輪につながっている。だからまっすぐな角材をつないだのでは作れそうにない。
　
　図3は、柱の前後関係が床と天井で逆転した構造を表している。これもエッシャーの作品「ものみの塔」（1958）の中で使われている構造を単純化したものである。

　　　　
　これらのだまし絵は、長い間、絵には描けるけれど立体としては作れない、と思われてきた。しかし、実際には、立体として作れるものがあることがわかってきた。そのきっかけは、絵を理解するコンピュータを作りたいという研究であった。
　
　私は、研究の中で作ったコンピュータソフトウエアの振る舞いを確かめるために、だまし絵も見せてみた。だまし絵は間違った絵であることをコンピュータがちゃんと判断するところを見たかったからである。
　
　しかし、期待に反して、コンピュータが、だまし絵を立体として解釈してしまうことがあった。調べてみると、ソフトウエアの間違いではなくて、立体として作れるだまし絵があることがわかってきたのである。