ド文系でも腹落ち｢微分｣を成り立ちから理解する ズボラな発想から緻密な予測をする数学が生まれた

微分積分という緻密な予測をするための数学が、このような「ズボラな」発想に支えられているというのが、微分のおもしろいところです。

まっすぐ飛んでいるとみなせるのであれば、話は簡単です。あとは、具体的にどの方向に飛んでいるのかさえわかればすべて解決します。結論を言ってしまうと、砲弾がどの方向に飛んでいるのかは、図表2－5のようにグラフに一本の線を引くだけでわかります。

（出所）『見るだけでわかる微分・積分』より

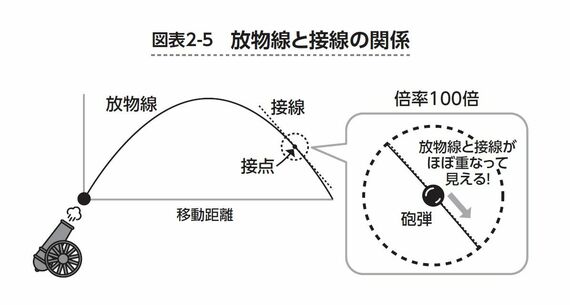
この線は、曲線（この場合は放物線）に接している直線で、数学の用語で「接線」といいます（“接している線”という意味）。この接線が、その瞬間に砲弾が飛んでいる方向を表しています。なぜそういえるかは、放物線をズームアップして見てみると分かります。

放物線と接線が接している点のことを接点というのですが、その接点の周辺を虫メガネで倍率100倍にズームアップしたのが図表2－5の右側の図です。

微分の発想

このように、ズームアップして見ると、放物線と接線がほぼ重なり合って、見分けがつかなくなっていますね。つまり、放物線そのものは曲がった線（＝曲線）ですが、その一部をズームアップすると、接線（＝直線）と区別がつかなくなるのです。

実は、これと似たようなことを私たちも日常で経験しています。私たちが住んでいる地球は、宇宙から見ると丸い形をしています。でも私たちは、水平な大地の上で暮らしていると感じているでしょう。

それは、私たちよりも地球の方がはるかに大きいので、球面上に住んでいることを実感できないからです。だからこそ昔の人類は、世界はお盆のように平らだと思い込んでいました。

それと同じように、全体としては曲線のグラフでも、その一部を虫メガネで拡大して見れば直線に見えるわけです。あるいは、自分がアリよりもずっと小さな小人になって曲線の上に降り立ったと考えてもいいでしょう。

地球に住む私たちが大地を平らだと勘違いしていたように、あなたは曲線のことを直線と思い込むに違いありません。この“ズームアップ”は、先ほどの“短い時間を考える”ことと同じ意味になります。つまりは微分の発想です。