ド文系でも腹落ち｢微分｣を成り立ちから理解する ズボラな発想から緻密な予測をする数学が生まれた

この研究がきっかけとなって、砲弾の軌道は放物線（＝ものを投げたときのアーチ状の軌道）と呼ばれる数式で表されることがわかったのです。

砲弾の軌道がわかれば、砲弾がどれだけ離れた相手に当たるかどうかも計算で出せます。つまり、どれくらい近づけば敵に命中させられるかが正確にわかるということなので、これは戦略的に大変有利になります。

砲弾の“進む方向”を知るには？

砲弾の軌道の研究はさらに進みます。

どれだけ遠くまで届くかが計算できるようになったわけですが、今度はさらに、砲弾がどの方角へと飛ぶかも計算したいというニーズが出てきました。というのも、砲弾が進む向きは時間がたつと変わっていくからです。

図表2－4のように、砲弾の進む方向（図中の矢印）はたえず変わっていきます。砲弾が敵の城や船に命中するとき、どの方向から当たるのかによってダメージも変わってくるでしょう。

（出所）『見るだけでわかる微分・積分』より

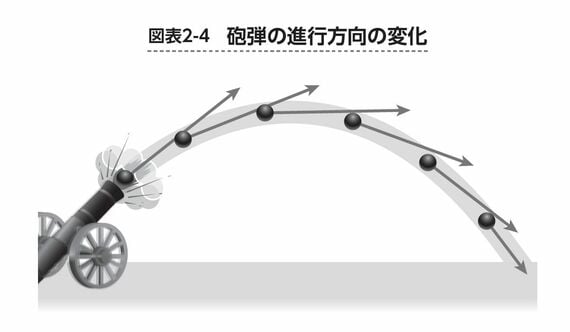
ですので、砲弾の進む方向（＝砲弾がどの方向から当たるか）がわかれば、より効果的にダメージを与える戦略を考えることができます。となると、砲弾の進む方向についても、数学を使って計算できるようになりたいですね。

すでにヒントはあります。というのも、先ほど話したように、砲弾の軌道は放物線と呼ばれる曲線（図2－4のようなアーチ状の曲線）で表せるとわかっているからです。

すでに砲弾の軌道のことはわかっているので、砲弾の“軌道”と“進む方向”の関係が分かれば、進む方向についても計算できるに違いありません。結論から言ってしまえば、「短い時間を考える」という微分の発想によって、この問題を解決することができます。

砲弾は、時間とともに飛んでいく方向が変わっていくわけですが、例えば0.1秒や0.001秒などの短い時間を考えてみましょう。それだけ短い時間であれば、砲弾が飛ぶ方向はほとんど変わりません。

より正確に言うと、実際は短い時間であっても少しは変わっているのですが、時間が短すぎて、無視できるほどしか方向が変わらないということです。つまり、非常に短い時間であれば、砲弾はまっすぐ飛んでいると考えてもよいのです。