｢未婚と既婚｣に立ちはだかる｢3.68人の壁｣の正体 結局､何人と付き合えば結婚までできるのか？

では、既婚男女は結婚に至るまでどれくらいの恋愛人数を経てきたのでしょうか。ご夫婦でも、相手が今まで何人と付き合ってきたかをご存じの方は少ないと思います。

そもそもそんな質問をしたら「なんでそんなことを聞くの？」と勘繰られ、質問に答えようが拒否しようが、結局面倒くさい場面しか生まれない予感がします。仮に、そういう話をオープンに言い合える関係性だったとしても、それが真実かどうかは確かめようがありません。

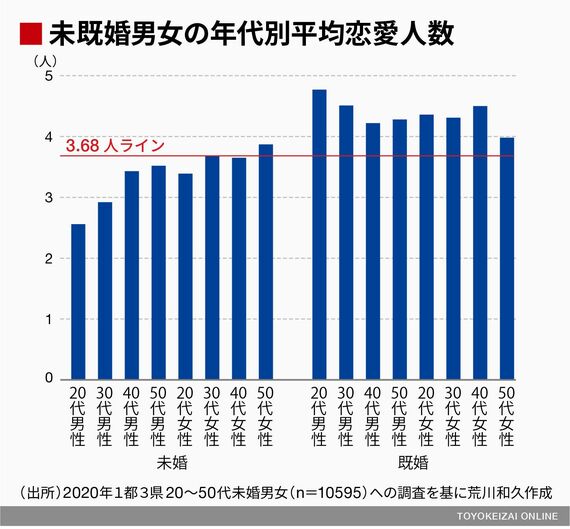
1都3県20～50代の未既婚男女約1万5000人に対して行った調査に基づき、未婚と既婚のそれぞれ年代別に今まで付き合ってきた人数（恋愛人数）の平均値を出してみました。それによれば、ある法則が浮かびあがってきます。それは、未婚と既婚とを分ける「3.68人の壁」です。

グラフにあるとおり、未婚男女の平均恋愛人数は、性別年代によって多少のばらつきはありますが、50代未婚女性以外はすべて3.68人以下です。一方、既婚男女はほぼすべて3.68人以上の恋愛人数となっています。

「36.8％の法則」とは？

これは、数学者マーチン・ガードナー氏などの研究者が提唱している「36.8％の法則」と呼ばれるものです。

例えば、結婚相手を探すにあたって10人の相手とお見合いする機会があったとします。しかし、10人を横並びにしてあなたがその中から1人を選択することはできません。実際の恋愛においても、10人同時に付き合うことはできないからです。

1人ずつ順番にお見合いして、あなたはその都度、そのお見合い相手と結婚を決断するか、次の相手に移行するかを選ばないといけません。お見合いを続けていく中で「この人に決めた」という決断をした時点で、残りの候補者とは会うことはできなくなります。

また、最後まで誰も選択しなかった場合は、10人目の相手と自動的に結婚することになります。10人全員を見てから、「やっぱり2番目の人がよかった」というわがままは許されません。

さて、そういうルールで結婚相手を決めなければいけないとしたら、何人目の相手を選択するのがベストな選択なのか、それを数学的に解明したのが、この「36.8%の法則」なのです。

候補者全体の36.8％を超えないうちは、お見合いを続け（候補者が10人のこの場合は3人まで決断しない）、そのあと、｢それまで会った3人の中でいちばんよかった人｣を基準とします。4人目以降で、その基準を上回る候補者にめぐりあったら、その人こそあなたが選ぶべきベストな相手である確率が最も高いということです。

これは男性に限らす、女性でもそうですし、就職採用などの場合でも同様です。この理論のもともとは「秘書採用問題」として研究されたものです。