算数も怪しい人が知りたかった分数計算の真髄 わが子に真似させたくない｢暗記（だけ）数学｣

いま取り上げた公式は途中に「通分」が介在しているが、それをほとんど無視して、この公式の丸暗記から分数同士の足し算を学んだ人たちがいる。

そういう人たちは、例えば1/5と2/3の和は、通分を意識することなく、いきなり、

1/5＋2/3＝（1×3＋5×2）/（5×3）＝13/15 ・・・（＊）

と計算する。そして、そうした学びだけを練習したのだろう。

だからこそ、公式を忘れると、

1/5＋2/3＝3/8

というような計算を平然と行う人たちが現れたのである。

また、公式を覚え間違えて、

1/5＋2/3＝5/15＋6/15（分子に間違いあり）

というような困った計算をする事例もある。

「通分」は図で表せる

ここで、公式を学ぶとき理解しておかなければならない「通分」をビジュアルで説明しよう（外部配信先では図を閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）。

いまの計算に関していえば、縦と横の長さの比が「5：3」の長方形をとる。その中に、縦と平行な線分2本と横と平行な線分4本を等間隔に引いて、長方形を5×3＝15個の同じ大きさの正方形からなるようにする。

長方形には5つの行と3つの列ができるが、その長方形全体を1と見なすと、小さい正方形は1/15である。

そして、1/5は長方形の最下段に並んだ3個の正方形であり、2/3は長方形の左から2番目と3番目の列に並んだ合計10個の正方形である。それらを見れば、式（＊）を納得できるのではないだろうか。

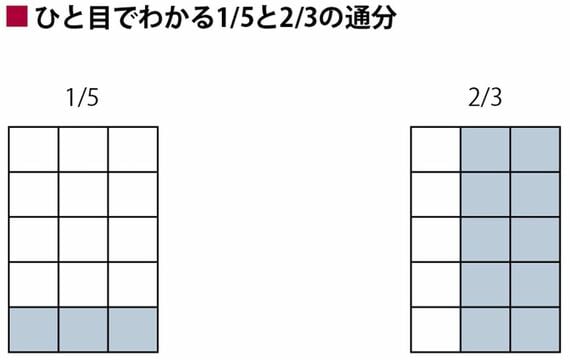
通分の仕組みを、一度はビジュアルで理解しておくとよいだろう。通分の理解の経験がないと、上で紹介したような誤った計算をしても、不思議に思わない人が現れてしまうのである。

もっとも、例えば下記の式でちょっと確かめると、「分母同士と分子同士を加えた和の計算式は変ではないか」と気づくはずなのだが。

1/2＋1/2＝（1＋1）/（2＋2）＝2/4＝1/2 ？？？