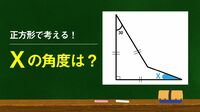
数字に強い人なら一瞬!「約数の理解」を計る問題 ほとんどの数に「約数が偶数個ある」のはなぜか

数字に強い人は「約数に対する感度」が高い
算数や数学ができる人は、「約数」に対する感度が高い場合が多いです。
約数とは、「ある整数に対して、その数を割り切ることのできる整数」のことです。10だったら2や5で割れるのでこれが約数になり、55だったら5や11が約数になります。
例えば「13/78」という数を見たときに、みなさんはすぐにこの数を約分することを思いつくことができるでしょうか? 78は13を約数に持っており、「78÷13=6」となります。ですから「13/78」は「1/6」なのです。
こういった感覚があれば、例えば「78人の参加者をどのようにテーブルに配分しようか?」といったことも考えやすくなり、実社会でもいろんなところで活用することができるのです。
そんな約分にまつわる、ちょっと面白い問題を紹介させてください。
「1の倍数番目の箱すべてにボールを入れる」
「2の倍数番目の箱すべてにボールを入れる」
……という試行を、100の倍数まで繰り返したとき、ボールが偶数個入っている箱はいくつか?
難しいですが、例えば6番目の箱で考えてみましょう。






























無料会員登録はこちら
ログインはこちら